Dimensional Gate Operators, Quaternion Multiplication & Gluon Structure

Christopher C. O’Neill

University College Dublin (UCD), Belfield, Dublin, Ireland

email: chris.ozneill@gmail.com

17 December 2020

Abstract

A model for gluon structure and the strong force is constructed based on previous research using DGO Quaternion Multiplication. That research proved effective for modelling all 18 quarks in the Standard Model and their various colour charges and their principle interactions, as well as the basic structure of gluons. Given how interrelated are the colour charges of quarks and gluons, the method is reapplied focusing (almost exclusively) on gluons and the strong force. The model uses a 4-dimensional rhombic dodecahedron constructed entirely out of DGO Quaternions and is shown to incorporate the Gell-Mann Matrices.

DGO Quaternion Logic

In ‘DGO Quaternion Multiplication, Quarks and Polyhedra’ the basic structure of the quark-gluon field was laid out. In that research, we were able to create the barebones model by which all 3 generations of quark were accounted for. Furthermore, we were able to account for the different masses of charge -1/3 and charge 2/3 particles and show how quark-anti quark pairs (mesons) were possible under the system without any difficulties.[1]

In this paper, I will do the same for gluons. Gluons are a different sprite-like entity to the quarks. For starters, they are, in a sense, their own anti-particles. They also self interact. Any model of gluons has to contain these features. It also has to be in accordance with the Gell-Mann Matrices, which have proven to be the simplest model for the colour charges of the quark-gluon model. The DGO Quaternions can model and account for these properties.

The reason for its effectiveness is that it is not limited to the traditional mathematical ∆ logic, but also incorporates: !∆, ^U and !VD logic.[2] This freedom allows for many different types of Quaternion Polyhedra to emerge from the same process — making the model simple, robust and beautifully tailored in its constructed.

With that said, let’s take a look at how DGO Quaternion Multiplication can model and explain the key features of the gluons, their colour charges, their particle-antiparticle-like nature, and their status as a self-interacting particle; before suggesting a model for their underlying structure and how it interacts with quark colour charge via the strong force.

The Cat and the Tesseract?

The gluon field is based solely on ^U (OR UP) and !VD (NOT AND DOWN) logic. It is the first set of polyhedra that we encounter, when we apply the ∆ (XOR) and !∆ (XNOR) logic set to the Quaternions: That is the Real Quaternions (or the Hamilton Quaternions that we know) and the Imaginary Quaternions (formerly called the Anti-Quaternions)[1]. The result is two identical 4-dimensional Rhombic Dodecahedrons. What is a 4-D rhombic-dodecahedron, you might ask?

It is a good question. Through my preliminary research of hyper-polyhedra on the internet, I could neither find a description nor a representation of a 4-dimensional rhombi-dodecahedron. I suspect that the lack of information or data surrounding this issue stems from the somewhat confounding geometry of this semi-regular Catalan Solid.

Unlike it’s more malleable cousins, the Platonic and Archimedean Solids, the rhombic dodecahedron (RD) has very peculiar orthogonal projections, which look variously like a cube, a stack of squares and something between a cube and a hypercube. This last observation suggests that the RD is, in some sense, a 4-dimensional object lurking as a 3-dimensional object. This characteristic of the shape always struck me long before I even knew its name or complete structure. The net of the RD also produces the most discombobulating Necker Cube effect that I have ever experienced, which has doubtless something to do with the fact that it is partially a 4-dimensional object living in a 3-d world.

Fig 1: This vertex-first-shadow of the tesseract forms a rhombic dodecahedron.[3]

The 4-d nature of the RD is demonstrated in Fig 1. The blurb, which accompanies this image on Wikipedia, states: “The 4D-hypercube, layered according to distance from one corner. As described in "Alice in Wonderland" by the Cheshire Cat, this vertex-first-shadow of the tesseract forms a rhombic dodecahedron. The two central vertices would coincide in an orthogonal projection from 4 to 3 dimensions, but here they were drawn slightly apart.”[3]

I’ve read “Alice in Wonderland” in both English and French, but I have no recollection of any mention of a tesseract by any of the characters. Be that as it may, any description of the Universe, which has its roots in the wisdom of Cheshire Cat and “Alice in Wonderland” must surely be on the right track.

We now have confirmation that our RD is in fact a 4-dimensional object. Indeed, this was obvious from the start, since it was created from the 4D quaternions. A tesseract is the confluence of 8 cubes existing at right-angles to one another. The Real Quaternion Multiplication over a range (-1, 1), produces a 3D projection of a tesseract with 33 unique points and 256 data points. Minus the central point, this is an 8-fold increase of data points over unique points. This 8-fold increase directly relates to the 8 cubes of the object formally described as a rhombic dodecahedron.

But, why do we minus the central point?

If we look at this next graph we see that the 16 vertices of tesseract can be numbered with the 4-bit binary numbers (or the 16 Dimensional Gate Operators). The two points in green (Fig 2) are meant to overlap and correspond to the XOR and XNOR logic gates. These two logic gates cancel each other out, reducing the number of data points from 264, to 256. This is more of an analogy than anything else. And more on this later.

Fig 2: The 16 logic gates as a power set over the tesseract vertices.[4]

A rhombic dodecahedron can be broken down into four rhombohedrons, in one of two ways. All eight hexahedrons appear in Fig 1 & 2. These 8 hexahedrons, as we shall see, are the 8 gluons of the Standard Model. Therefore, four gluons are represented in this model by a shape similar to a rhombohedron and the other four are cubes.

Fig 3: An isolated gluon.

We can easily take steps to isolate a single gluon, by simply taking steps of our rhombi-dodecahedron. There are 65536 points in the range(-2, 2) Real Quaternion gluon. Using a step range of 1024 results in a rhombohedron shape (see Fig: 3.1)

Fig 3.1: A gluon isolated from the Real Quaternion Rhombic-dodecahedron.

In Fig. 3.2, we see the isolated gluon in the context of the Real Quaternion rhombic-dodecahedron. While the geometry looks like a rhombohedron, it is just a cube viewed from a vertex-first perspective in 4D space.

Fig 3.2: A isolated gluon embedded in the Real Quaternion Rhombic-dodecahedron.

Fig 3.3: The rhombic dodecahedron made from the Quaternions

Quaternion Logic

We know that ^U and !VD are the logic gates that govern the Quaternions and we can see them in Fig. 2, directly beneath and to the sides of ∆ and !∆. Before we can delve deep into the mysteries of the gluonic field, we need to understand these a bit more and their relationship to the Quaternions. The Quaternions are given by William Hamilton’s famous set of equations;

i² = j² = k² = -1

ij = k, ji= -k

jk = i, kj = -i

ki = j, ik = -j

And correspond with, the following logic tables:

Fig 4: From left to right, top to bottom: !VD, ^U, and !VD and their corresponding quaternion algebras.

You might be wondering why these logic gates and why in this order? The ^U and !VD logic gates are chosen because they are non-commutative i.e. A(-B) =/= -A(B) and also because they satisfy the conditions of XNOR, where the rules of multiplication and division are inverted. This inversion explains and allows for the √-1 or i, which is a principle value in all hyper-dimensional spaces of this kind.

Both gates ^U and !VD are needed for quaternions, because sometimes AB equals a minus and sometimes it equals a plus and vice versa. Starting with the !VD gate then, we see that the first set of 0s is made equivalent to i, while the 1s are made equal to j. Since j = 1, this means that in ^U, k must be 0. In the third and final set, k is once more zero, which means that i = 1. This switching of i from 1 to zero closes the algebraic loop.

Gluons and Anti-gluons

Now that we understand the logic of the Quaternions and how they are constructed, we can begin to examine them in terms of the properties of gluons. One of the key features of gluons is that they exist as sets of particles and anti-particles i.e. they are their own anti-particle. In ‘DGO Quaternion Multiplication, Quarks and Polyhedra’, we showed how it was possible to convert an ordinary quark into an anti-quark simply by ∆ multiplying its Quaternionic matrix by an equal-sized matrix filled entirely with the value -1. XOR multiplication is permitted here, because we have already summed and multiplied the matrix down to the ∆ Quaternions or the !∆ Quaternions.

However, in the case of the gluon-rhombic-dodecahedrons, we are still at the level of ^U and !VD logic. Therefore, if we attempt to create an antiparticle out of the rhombic dodecahedron using the same -1 matrix, we must multiply by !VD or ^U (depending on whether the multiplication is deemed left or right). When we do this, any value that was -1 will remain -1 and any value that is +1 when multiplied by -1 will be a +1. As such, no change takes place and we can say that the entire gluonic system is its own anti-particle. Said another way, the !VD and ^U -1 matrices are identity matrices of the gluons.-1

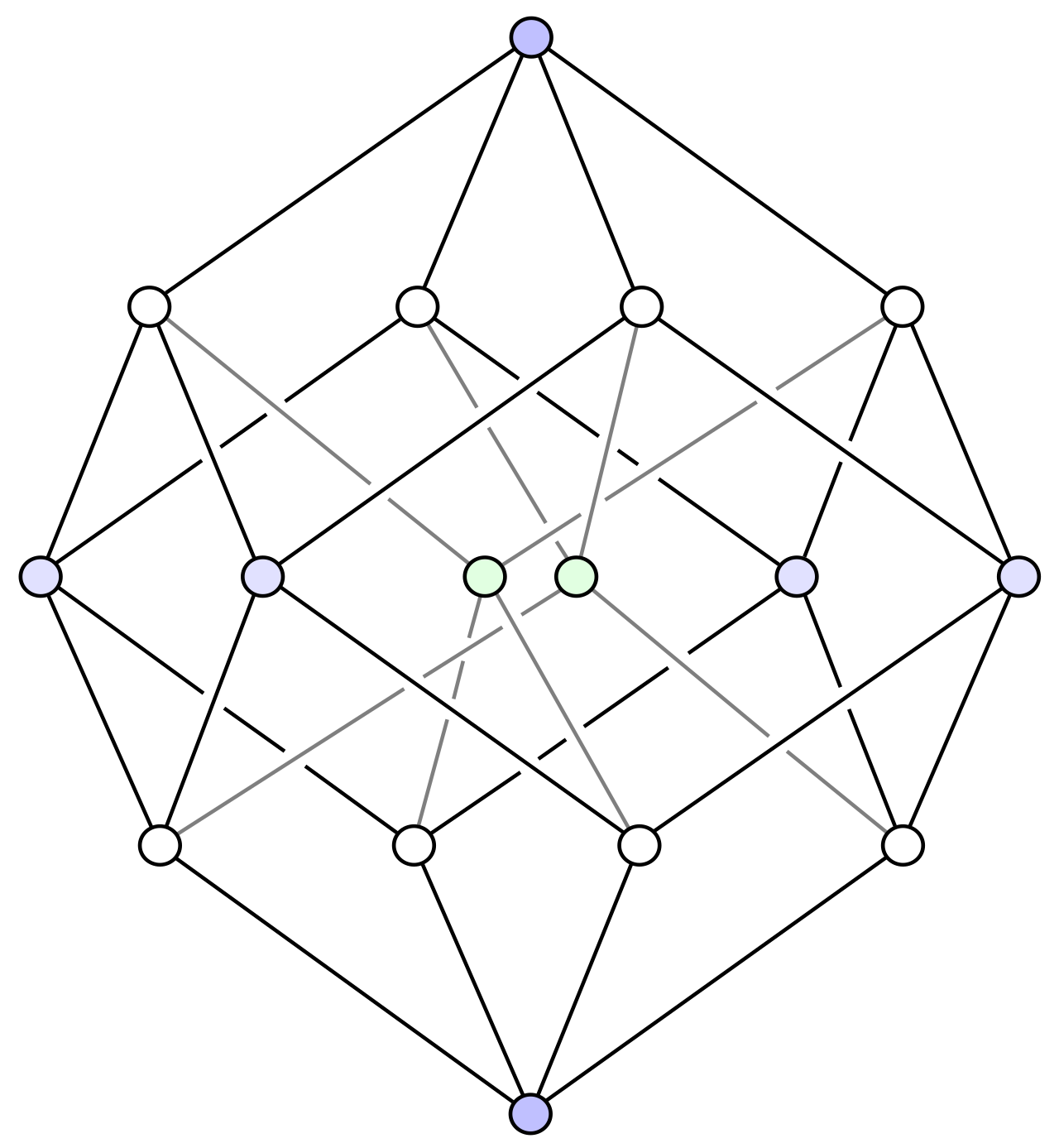
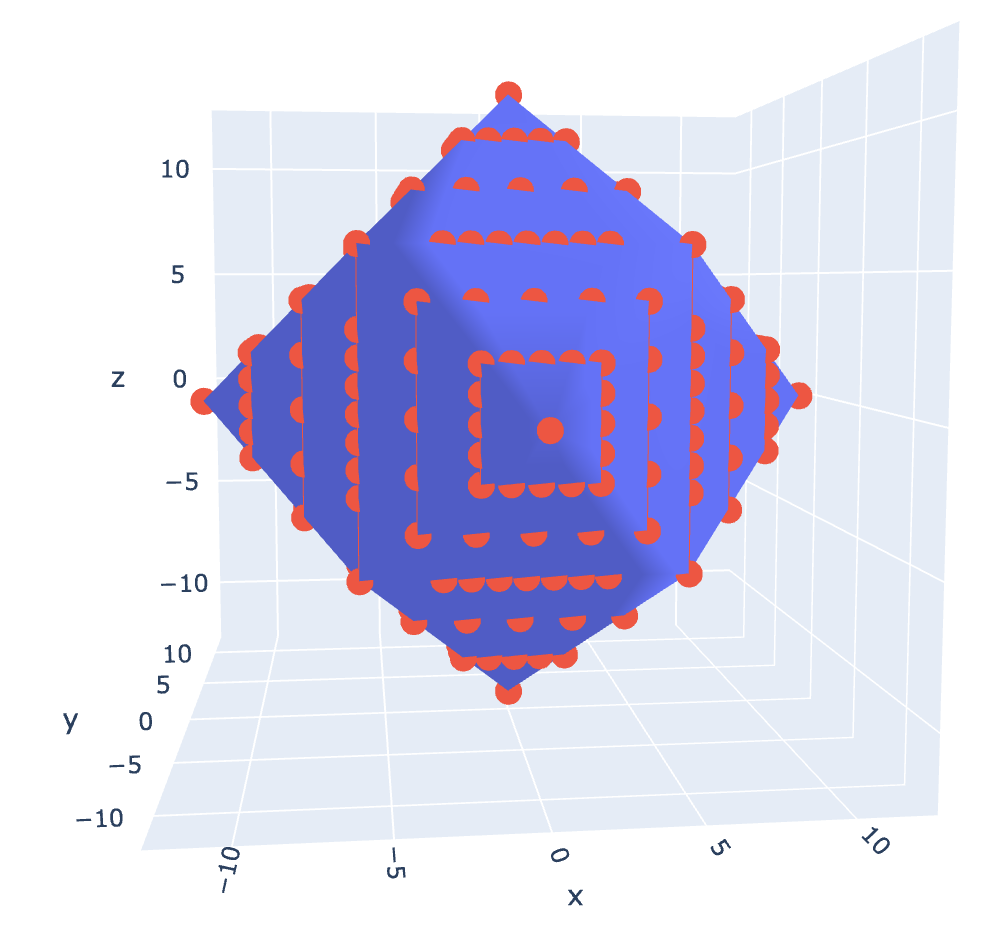
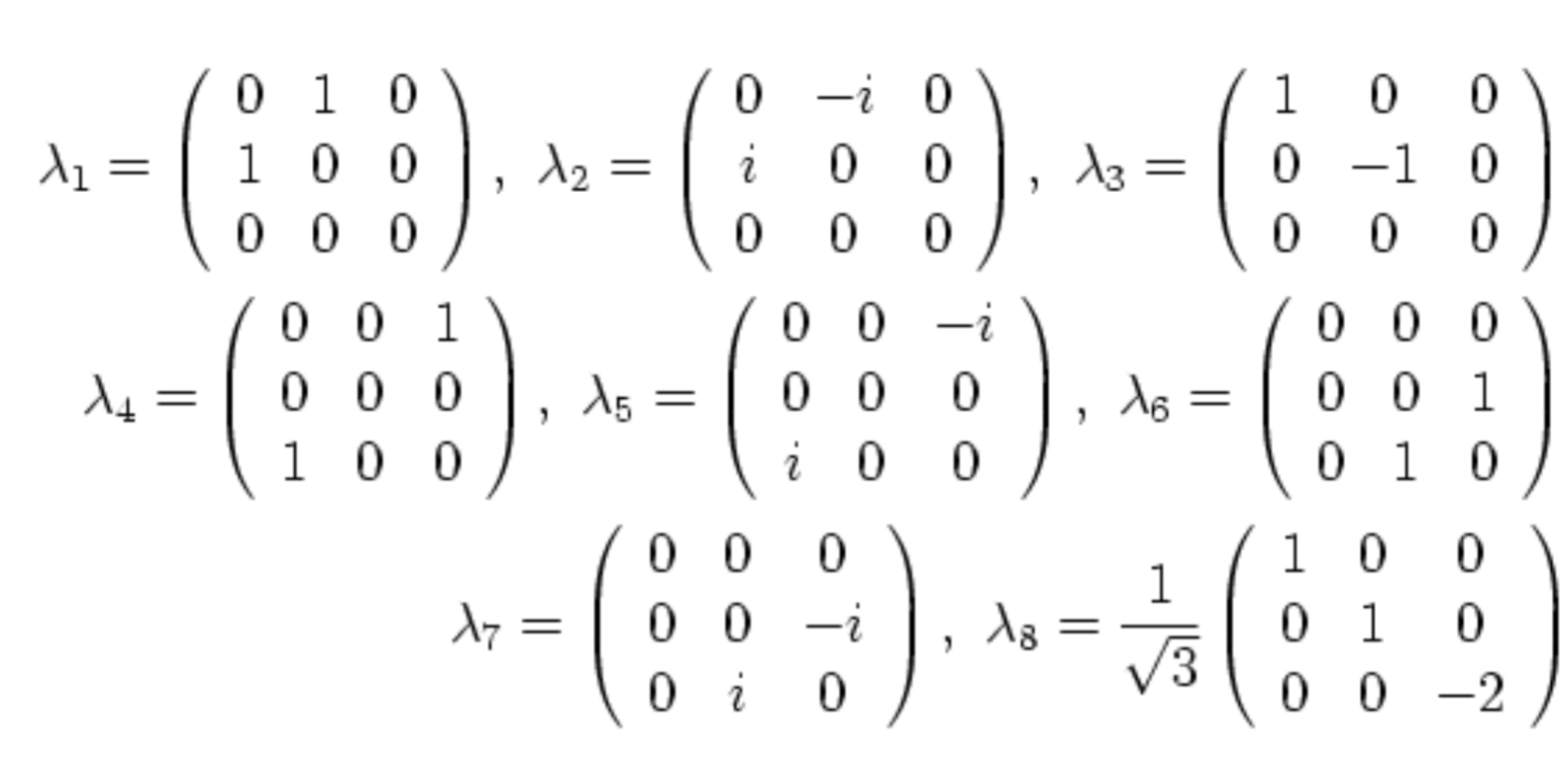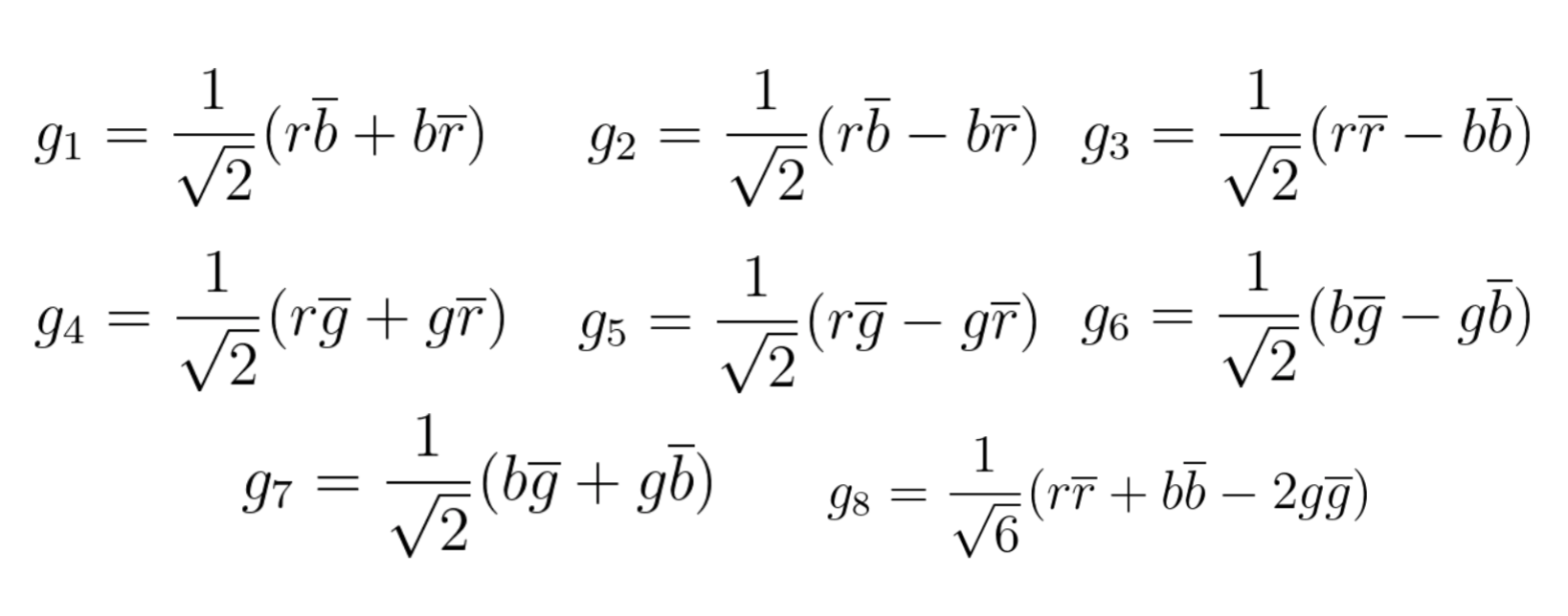Fig 5: ^U matrix multiplication of the Quaternions by -1 matrix also equals the Quaternions

A related aspect of the gluon anti-gluon model arises from their ability to self-interact. This self-interaction (or Strong Force) is an expected consequence of the interrelationship between the rhombohedrons in the tesseract model of the gluons. Over short distances, there isn’t that much of the gluonic field, so the interconnections are fewer. But, as the field is stretched (for example, when attempts are made to pull a quark out of its confinement) the area that the field takes up also increases, which increases the number of connections and therefore increases the strong force (or flux tube)  holding the quarks in place.

For this reason, it is impossible to break the quarks out of their confinement. A visual description of this action is easy to obtain using Quaternion gluons, and two XORed cube quaternions, which represent two u quarks. All we need to do is increase the distance between the up quarks and increase the range and orientation of the gluon connecting them. (Fig. 7 & 8)5.

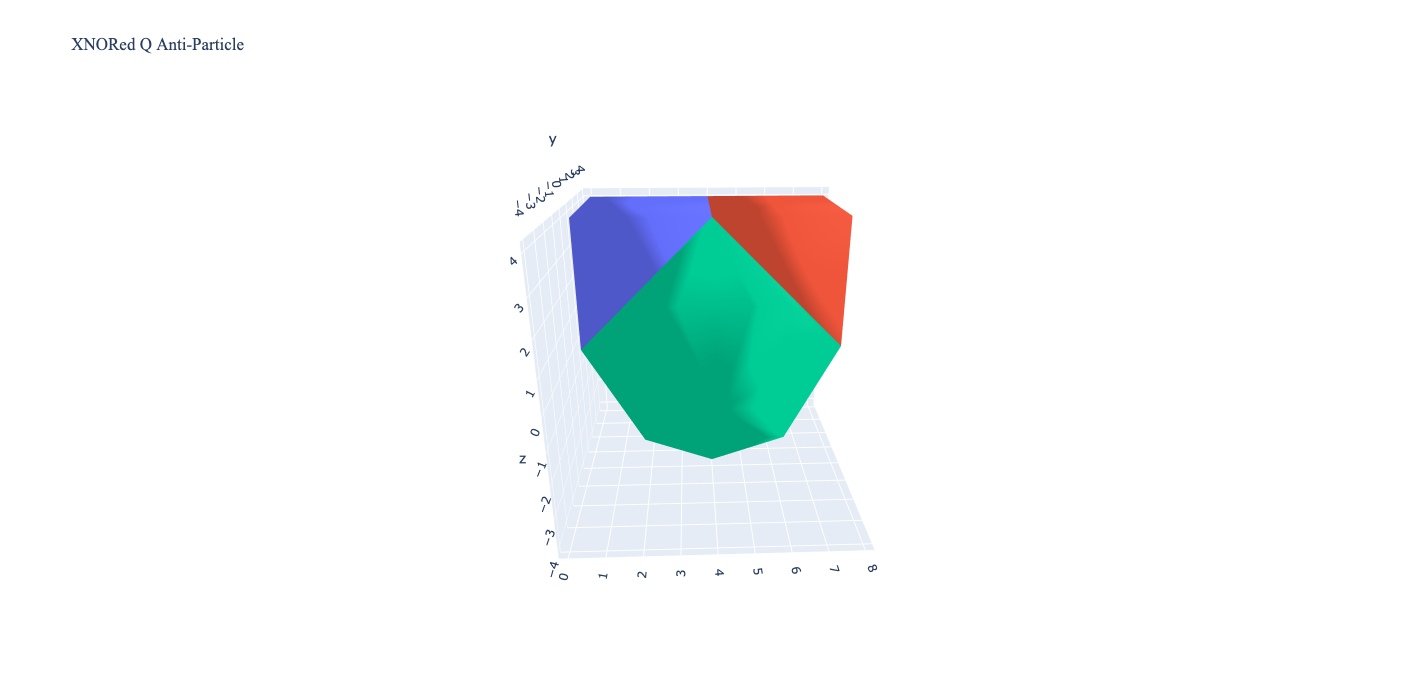
Fig 5 & 6: A meson made from a red and a blue quark, connected by a gluon.

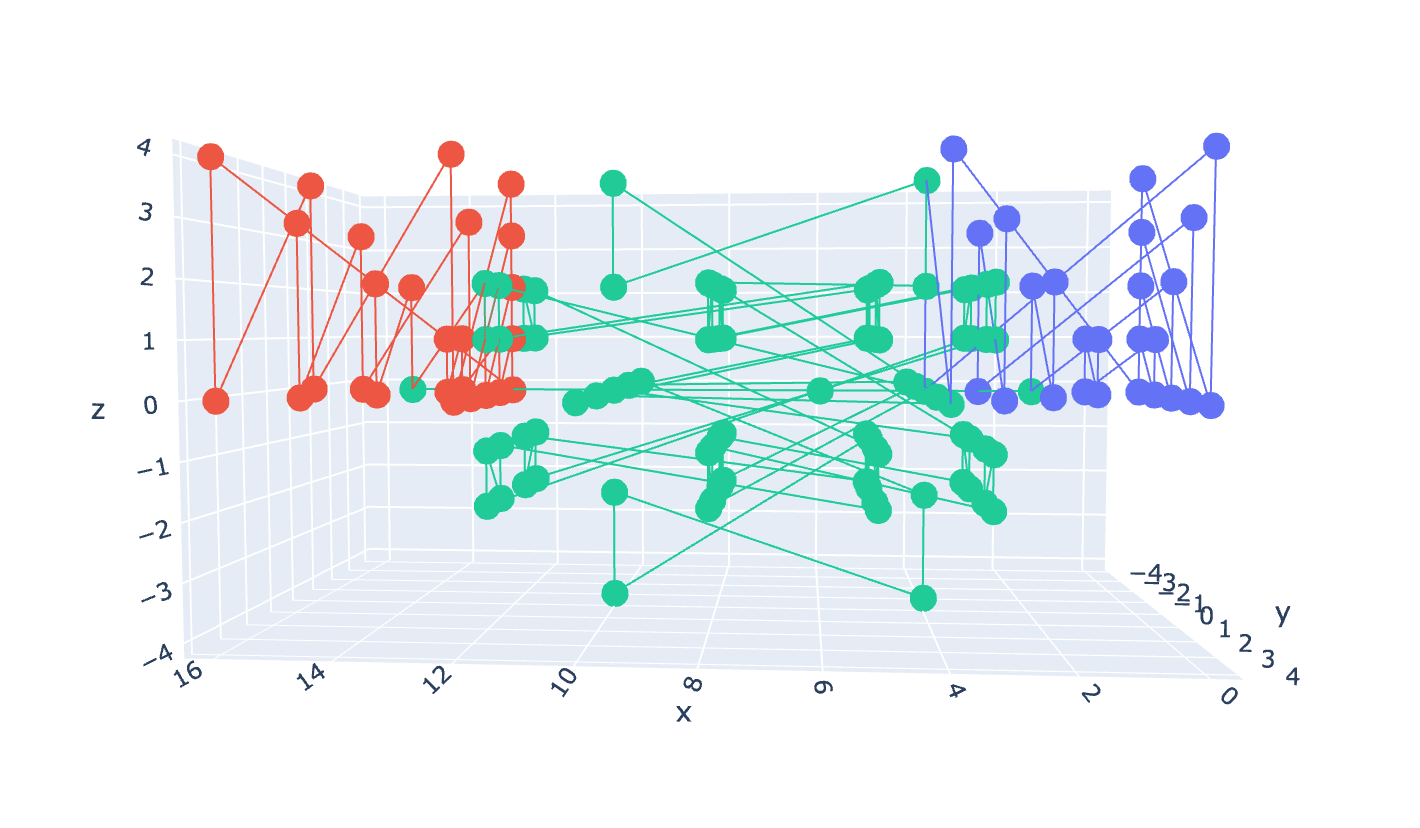
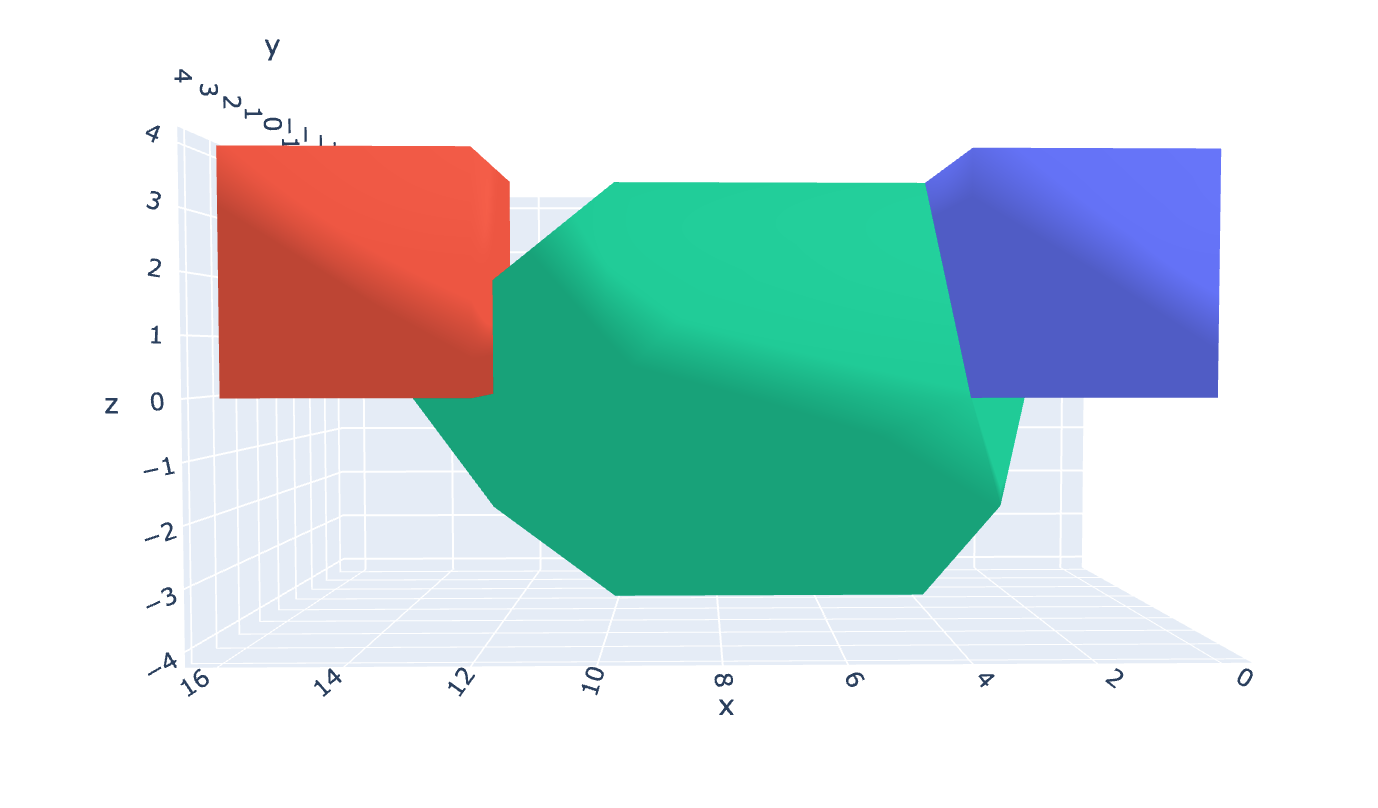
Fig 7 & 8: Normal stretchy behaviour of the gluon.

Fig 5 and 6 show a meson (in this case its two up quarks) bound together by a gluon. Other arrangements of this meson are possible, but this is how the meson looks ‘out of the box’, so to speak. As the quarks jiggle around inside the nucleon (See Fig 7 & 8), the gluon begins to spread but there isn’t a notably increase in size or connections. Either way, to stretch a gluon, the range needs to be increased and the orientation of the gluon needs to be changed from (i, j, k), to (v, i, j), where ‘v’ is the vector component.

This represents a rotation, which in turn suggests a colour change of the gluon and therefore of the connected quarks. This suggests that the colour change of the quark and gluons is a direct result of the particles jiggling inside the gluon enclosure.

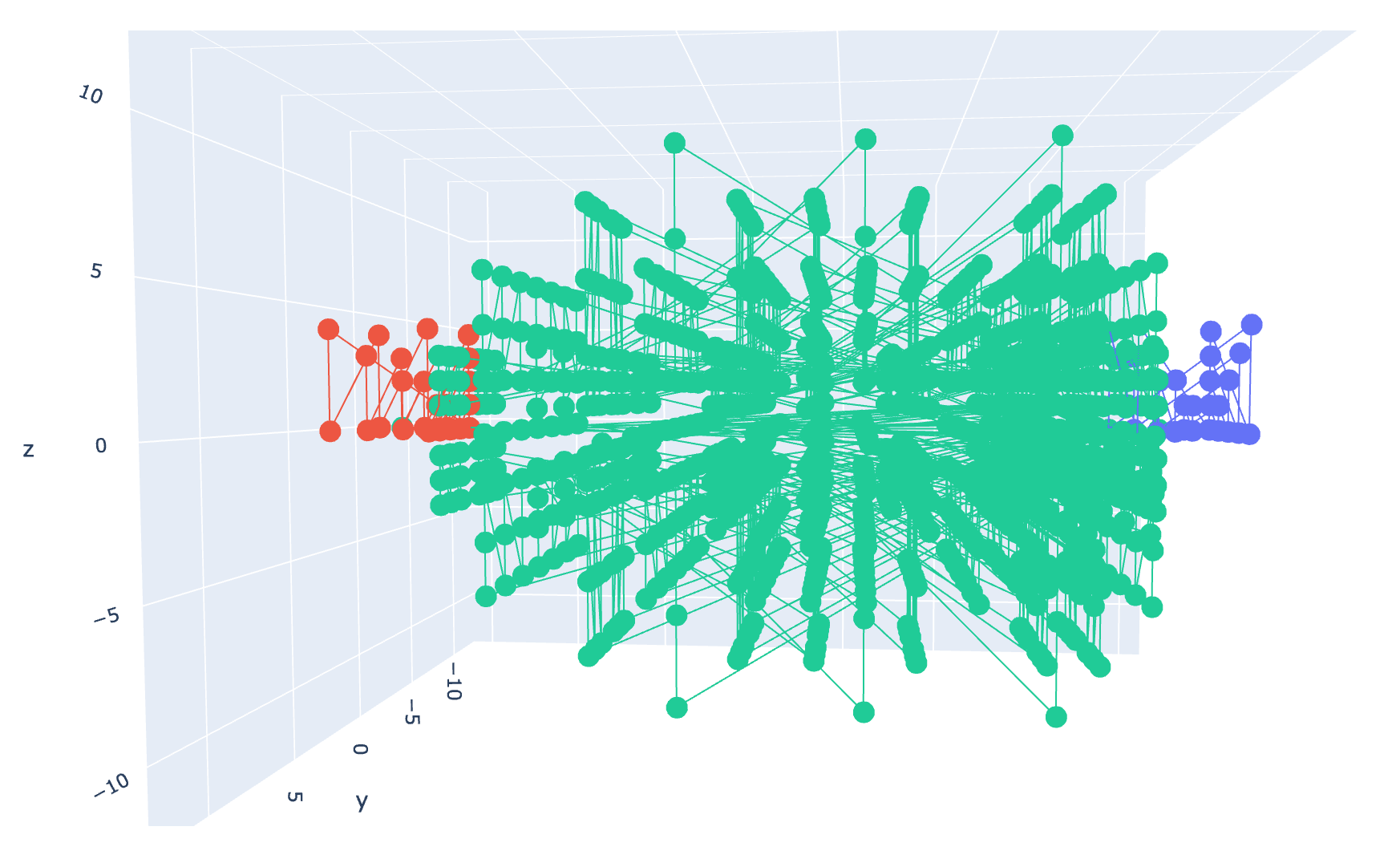
Fig 9 & 10: A red up quark being removed from a meson. The green anti-blue gluon begins to expand rapidly and the interconnections increase appropriately.

If an external force is applied to the meson (Fig 9 and 10), we see a dramatic increase in size and interconnections. This represents an increase in the Strong Force pulling the quarks back together again.

If we compare the results of this experiment with Derek B. Leinwebber’s visualisations of the same, we see many similarities and a few differences. Leinwebber refers to the green-blue regions between the two quarks as the “infamous flux tube”. [5]  This is equivalent to the gluon in the model above.

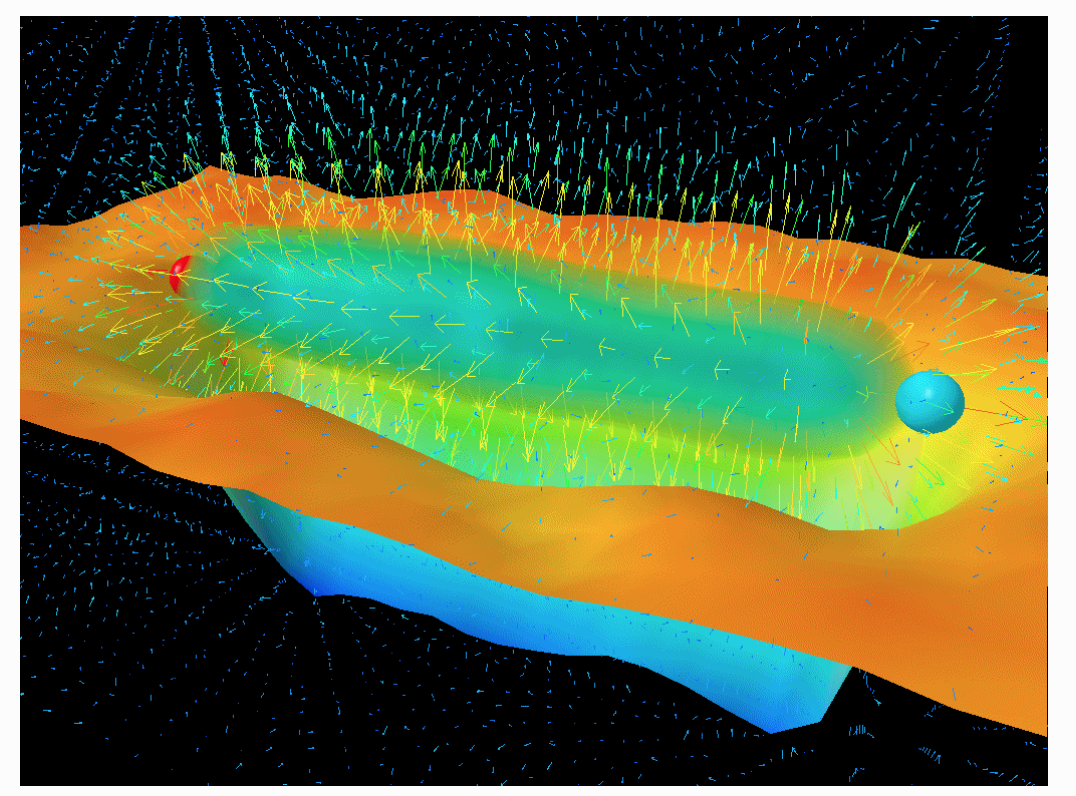
Fig 11: A still from Leinwebber’s animation showing the expulsion of the QCD vacuum between two quarks. [5]

One of the differences that is most apparent is that the diameter of the flux tube remains “approximately” the same, despite getting longer. The reason why we don’t see this happen in Fig 5-10, is because I was increasing the range across all axes, instead of solely in the direction of force, as I should have been. I have corrected this in the following graphs: Fig. 12-16. This results in seemingly less connectivity in the gluon structure overall, but it makes more sense, as the quark is being pulled in a single spatial direction. 

A consequence of the proposed model appears to suggest that any attempt to break quark confinement leads to a rotation of the gluon. According to QCD, a change in charge colour relates to a rotation matrix in one of Gell-Mann’s 8 matrices. From this perspective, a rotation would lead the green-blue gluon to change into a red-blue gluon (for example), which in turn would have a knock on effect on the adjacent quarks. Or does it?

Fig. 12

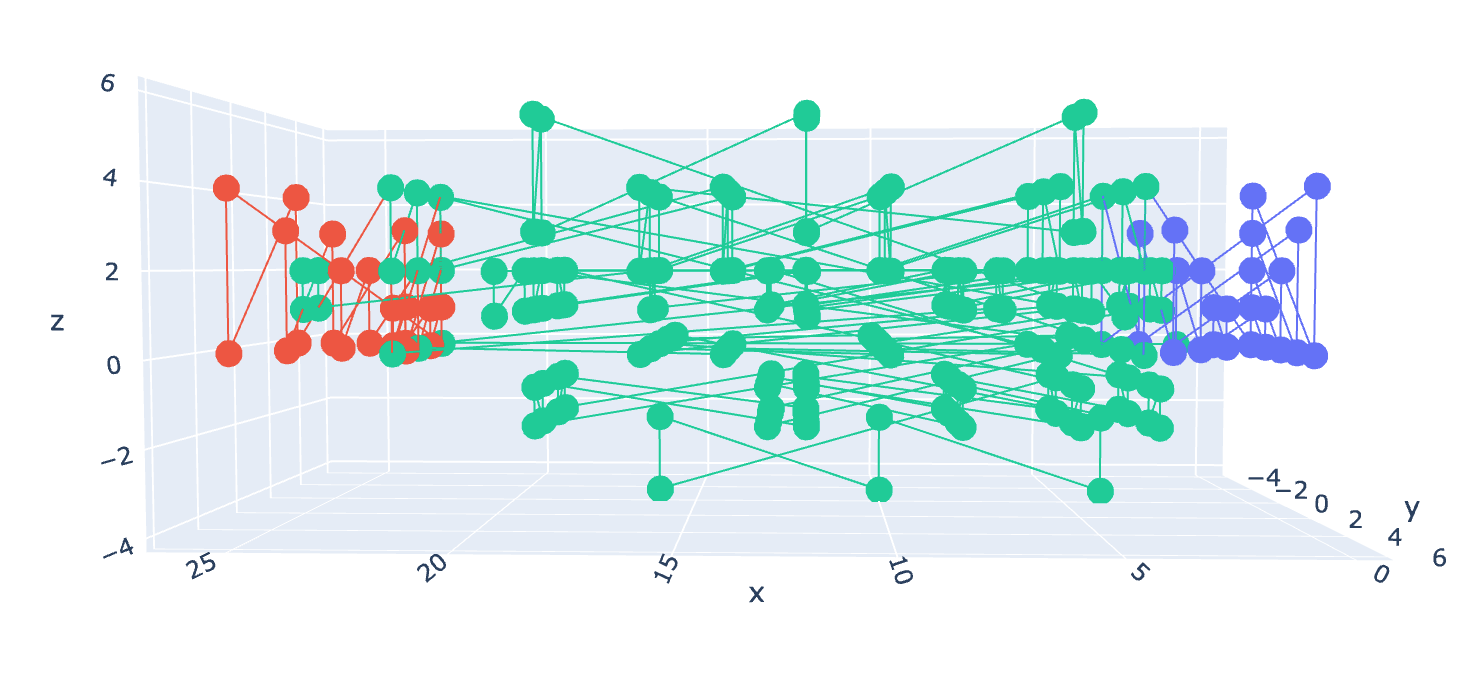
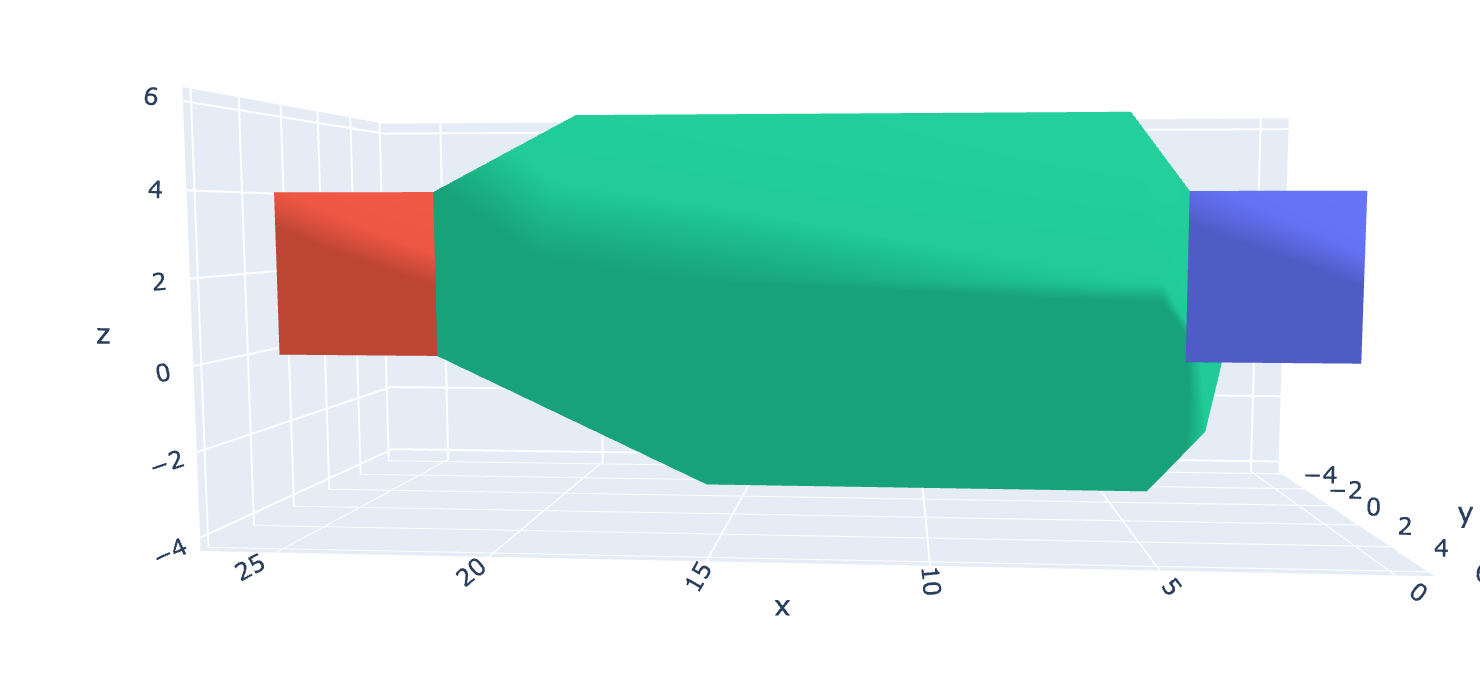
Fig. 13 & 14

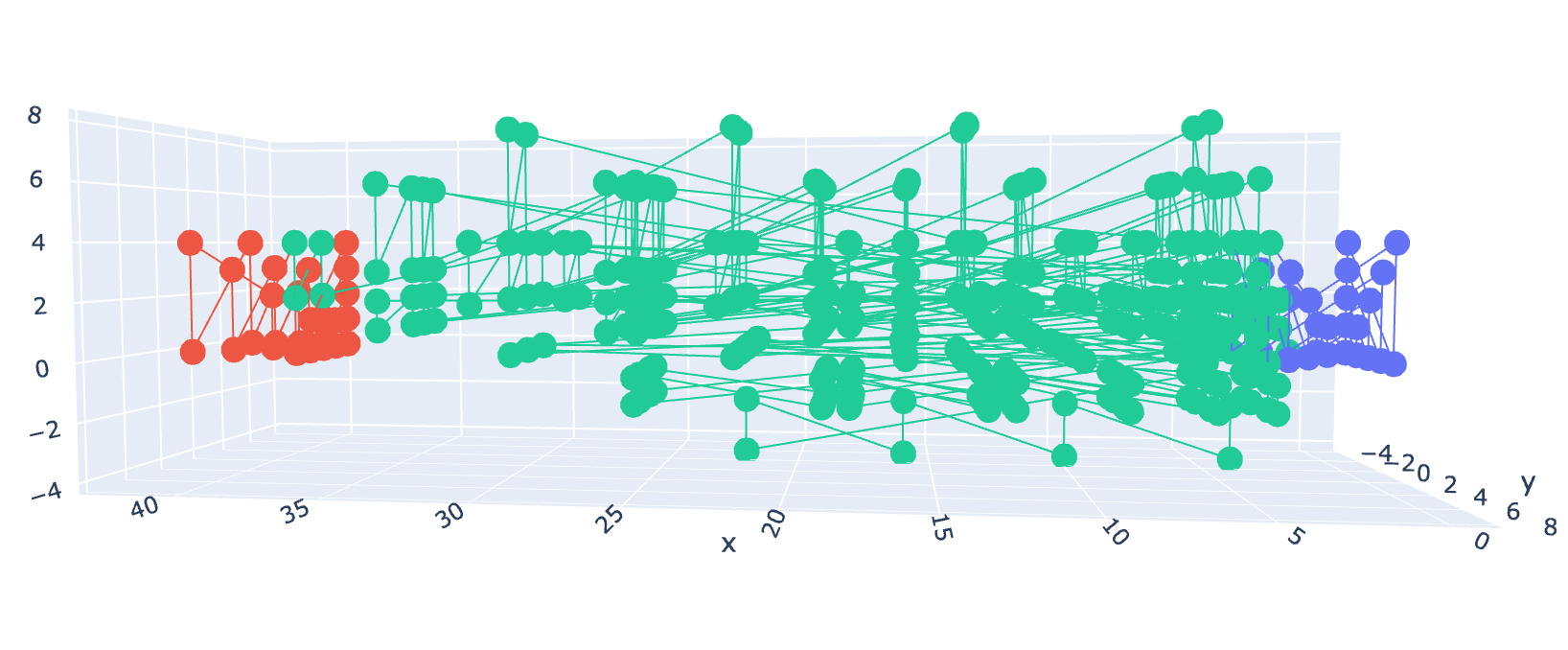
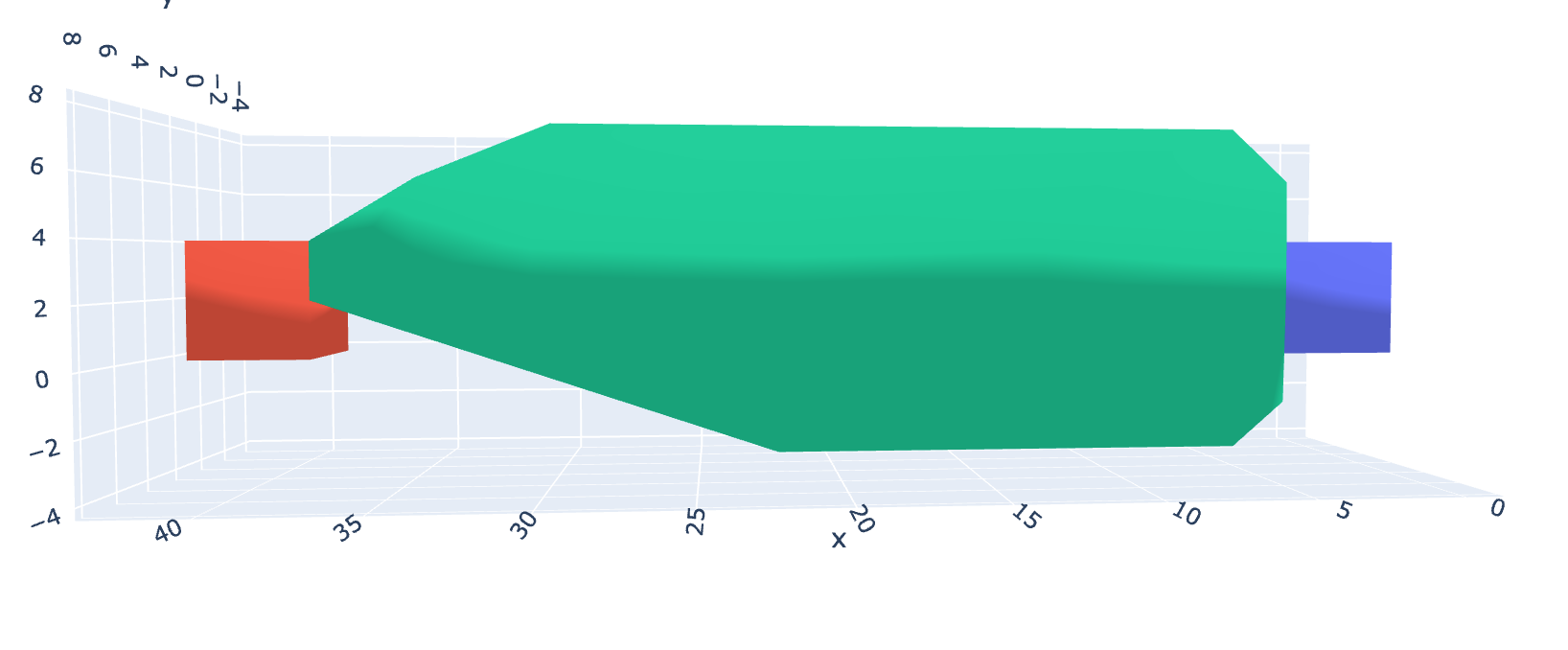
Fig. 15 & 16

Another potential problem with this visualisation is that we are looking at too many dimensions. We should only see one gluon, which we said was a rhombohedron, instead of the 4 to 8 gluons that we do see. Curiously there is no need to rotate an isolated gluon in order to stretch it (See 16.1).  I don’t yet know why that is, but it certainly simplifies the model, which is something that we obviously want.

Fig 16.1: A stretched gluon (or fluxtube) isolated from the RD

Since we have already arrived at the subject of quark and gluon rotations and their relationship to the Gell-Mann Matrices, now might be a good time to investigate this matter in a little more depth and detail.

Cog Colour & Gear Changes

Based on the research done in “DGO Quaternions, Quarks and Polyhedra” we know that the ∆ Quaternions and the !∆ Quaternions produce two identical rhombi-dodecahedra (RD). Based on the research in this paper we know that that RD is actually the vertex-first perspective projection of the hyper-cube. But looking at Fig. 12 through 16, we see that the u quark is also a 4-cube. Why are there two hypercubes?

The answer is that the u quark is a cell-first perspective projection. This implies that there is some kind of preferred perspective choice on how these particles present themselves to us, at least from the point of view of our Universe.

When generating the two RDs at the beginning of the process, we can naively think of them as 3D objects. This gives us three directions, which we will label red, blue and green (for x, y, and z) for the ∆-RD and 3 for the !∆-RD, which are kind of like the anti-gluons. This gives a total of 6 axes. When we multiply these three axes together we get 9 gluons — at least to begin with.

Where can we put these 9 gluons?

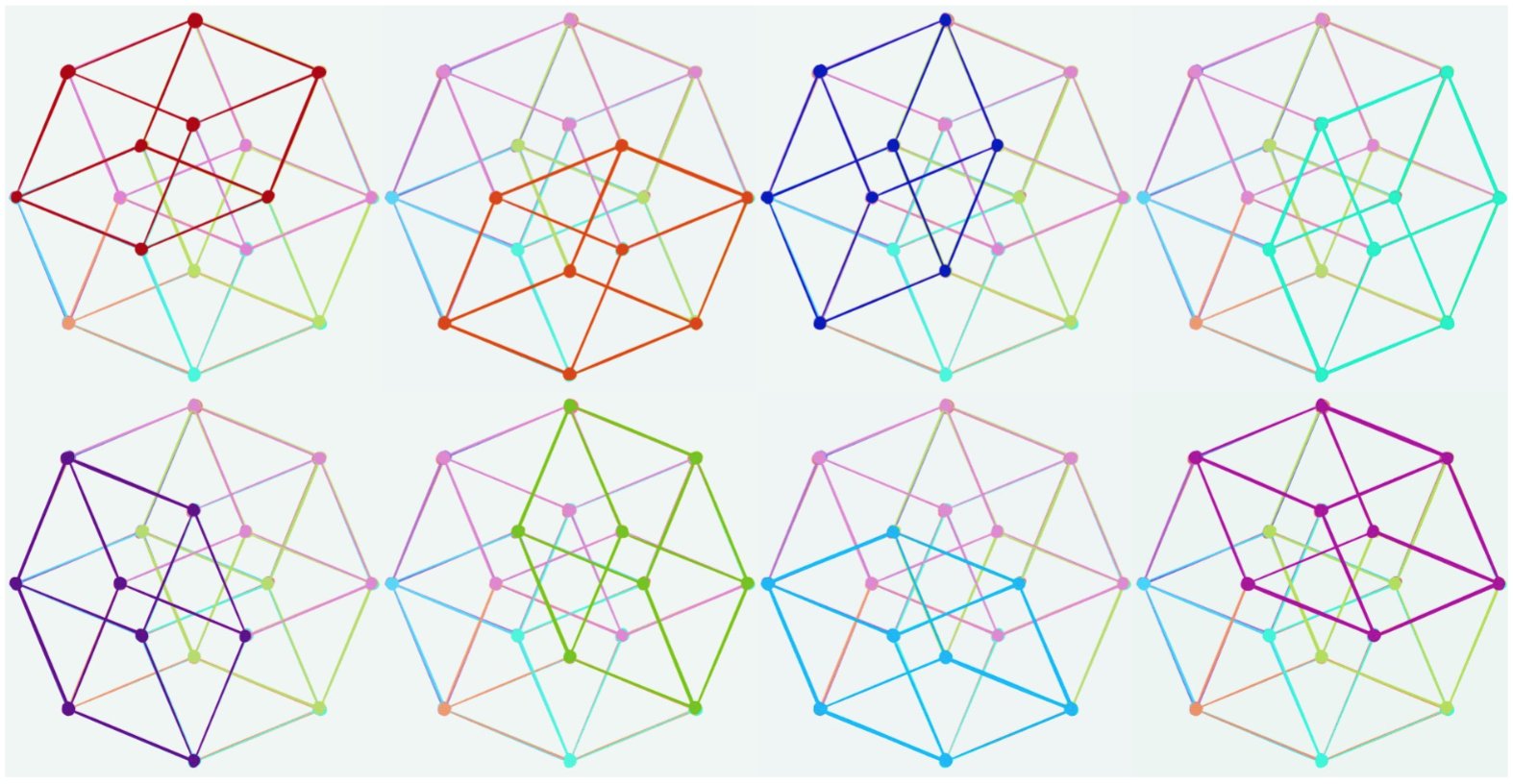
Fig. 17: All 8 gluons represented as the 8 cubes of the tesseract.

We can’t put them in the vertices of the RD, there’s too many, or in the edges or anywhere else. But we can put them in the cells. There are a total of 8 cells, so this means that we have to crush two of the gluons down into one.

But why are we allowed to do that?

A similar process is undertaken with the Gell-Mann matrices (Fig. 18), where the 9 gluons are mapped to SU(3).

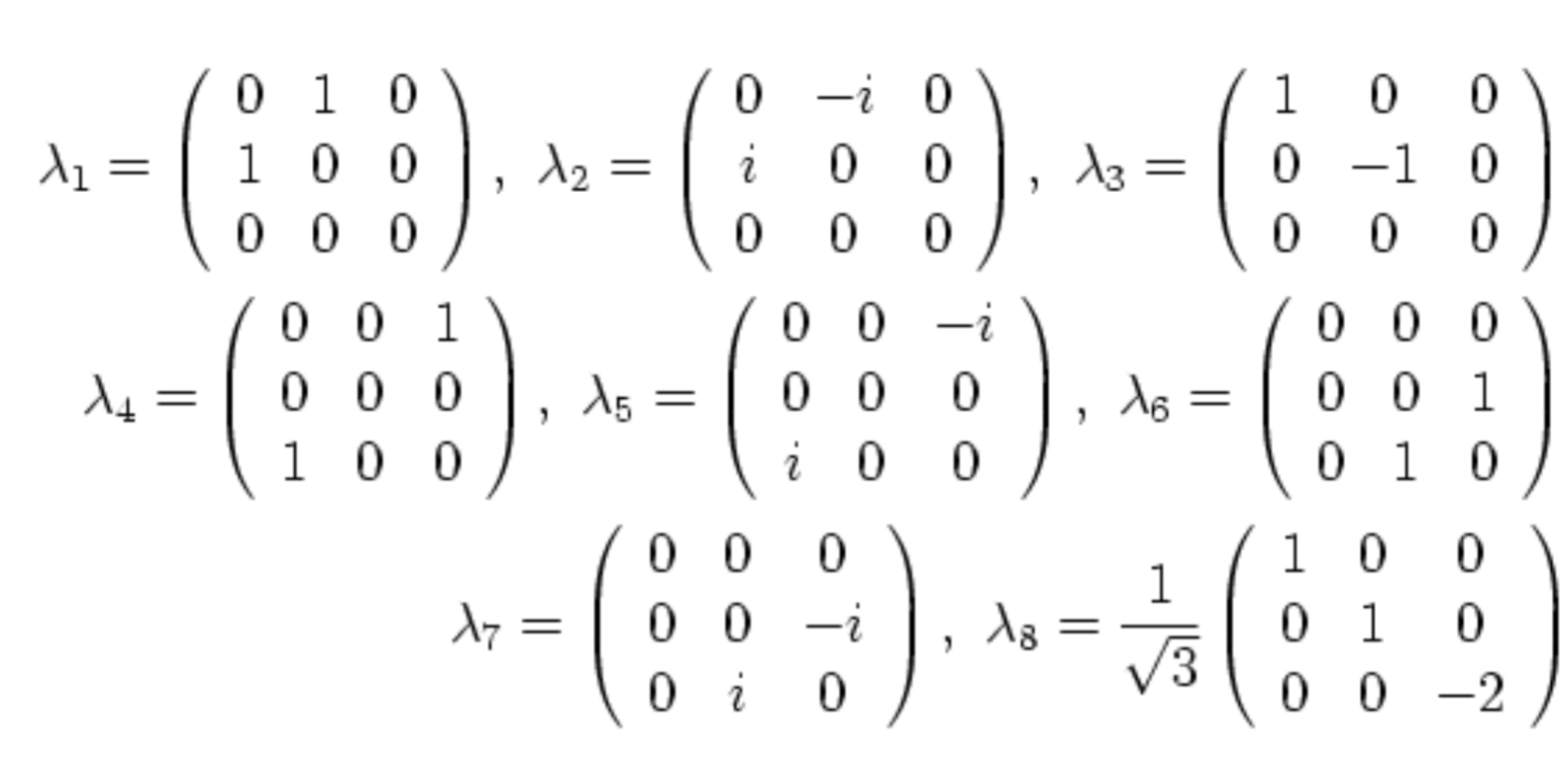
Fig. 18: The 8 matrices of SU(3)

Recall that there are 4 rhombohedrons in the vertex-first projection. Each of these has 4 vertices - making 16 vertices total. Now recall that there are 16 logic gates also mapped to these vertices. Two of these gates representing ∆ and !∆ are superimposed. This means that for each rhombohedron (or gluon) there are 9 gates mapped down to 8. We see precisely the same property in each of the 8 Gell-Mann matrices. Three of the gluons are not linearly independent, meaning only 8 of these are accessible.

Therefore, we can also map each of the SU(3) matrices to the 8 rhombohedrons in our hypercube. 

The Gell-Mann matrices are a mathematical construct, and an extension on the Pauli Matrices for spin-1/2 particles. Their construction comes about by necessity. They are meant to account for all of the characteristics that we see in quark gluon interactions. They need to be a 3-dimensional representation of 3 particles, whose internal symmetry gives rise to a neutral combination (i.e. a baryon).[6] Just like the Pauli Matrices, SU(3) finds its application in the realm of particle spin probabilities (See Fig. 19).

But just because they are purely abstract in character, doesn’t mean that they can’t be applied to something less abstract. Indeed, this is their entire reason d’être, to model the gluon colour charges, which are real physical properties. Therefore, it doesn’t appear to me to be overtaxing to assign them cells within the hyper-cube model of the Quaternions.

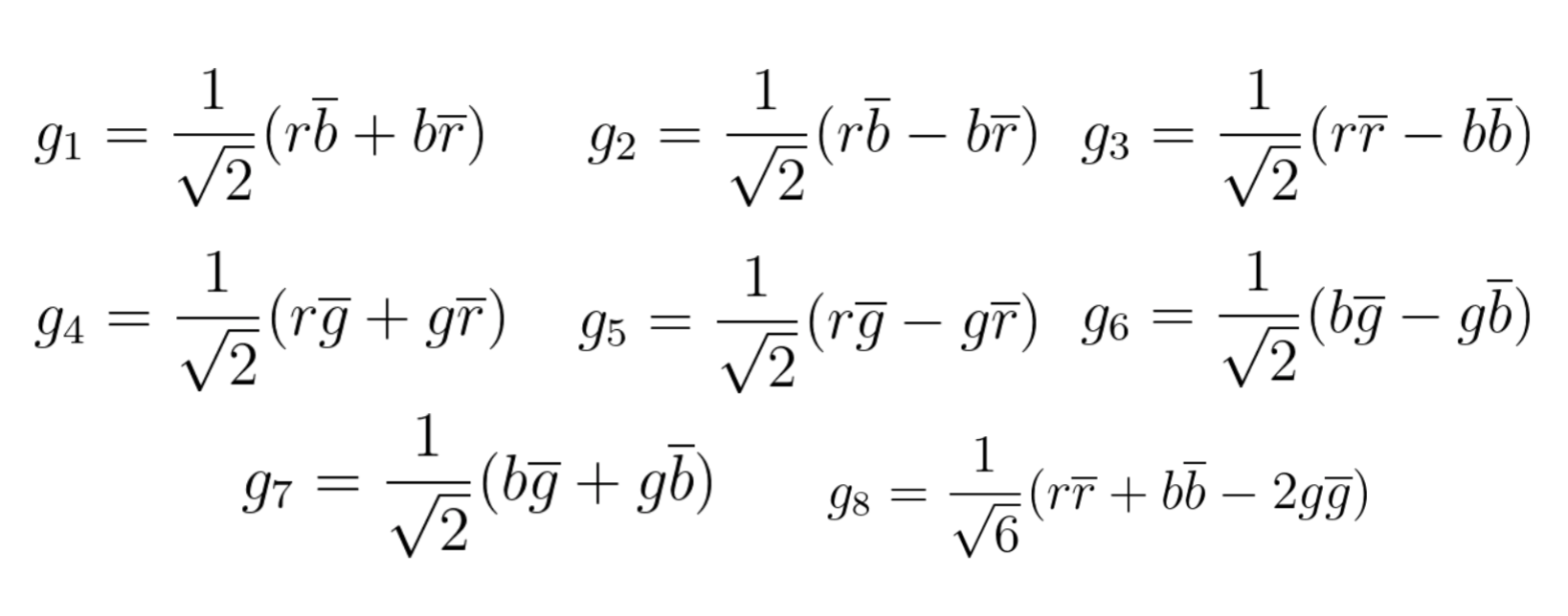
Fig. 19: Matrix multiplication between colour basis vectors and colour charges in SU(3)

In Fig 19 we see the equations for the probabilities of the gluon spin matrices. We can apply these equations to the 4cube model, along with our SU(3) matrices. By doing so, we turn a purely abstract set of 8-dimensional matrices, into lucid 4-dimensional object, with dimensions x, y, z and w viewed from a perspective in 3-dimensions (See Fig. 20).g₁

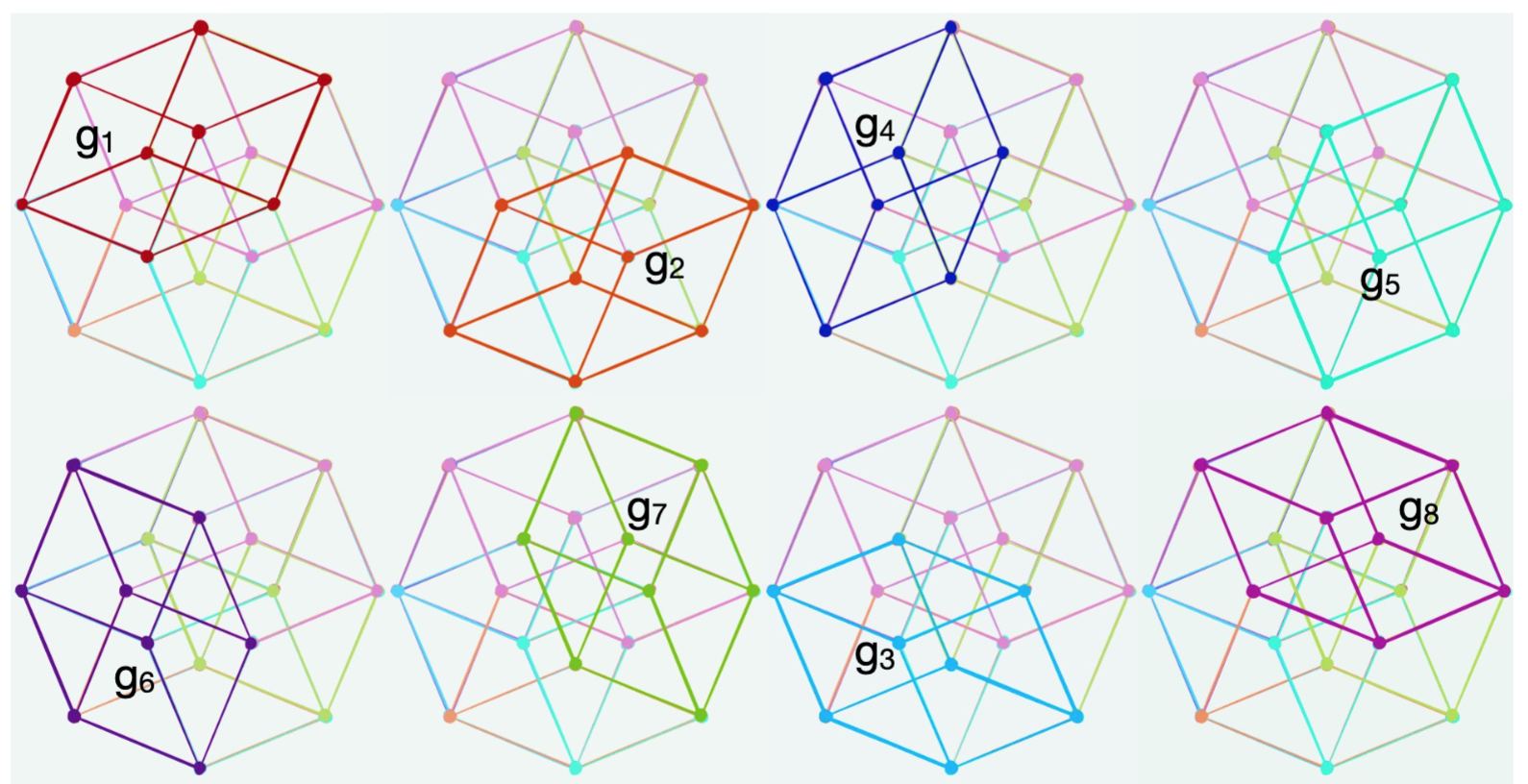
Fig. 20: The 8 equations g_n applied to the hypercube.

It should be possible to explain the sequence of colour changes within a nucleon with this model. This method could also be applied to the findings of the Stern Gerlach experiment, where the results of measurement of spin states are diminished or filtered out completely depending on which axis is measured. Filtering of a spin state, in this model, would equate to a reduction of dimensions about which the hypercube can rotate. More work needs to be done to show the model holds true in either case, although it will have to be left for another time, as we have enough to focus on with the structure of the colour changes in the quarks and gluons, for the moment.

From the point of view of the quark, we have to take into account the basis vectors (r, g, b) of the gluon. These basis vectors coincide with the colour charges of the quarks. This makes sense because the QCD of the gluons affects the colour charge of the quarks. I am going to argue that this affectation is achieved through entirely mechanical means, which is ironic because this subject is called ‘Quantum Mechanics’. The analogy I would use is like a set of cogs or gears; a rotation of one inter-dimensional particle around an axis can result in a change in another, although not always, as we shall see.

Rotations

To date, we have discovered our rhombi-dodecahedron (RD) was actually a vertex-first projection of a 4cube and our u quark was actually a cell-first projection of a different 4cube. Now, we are going to flip that and have the RD as a cell-first projection and the u quark as a vertex-first projection. This precondition will help us better explain what’s going on. Recall that we are viewing these systems in the 3rd dimension now, so they will both just look like cubes. Or, if you prefer, a 2-dimensional topological surface.

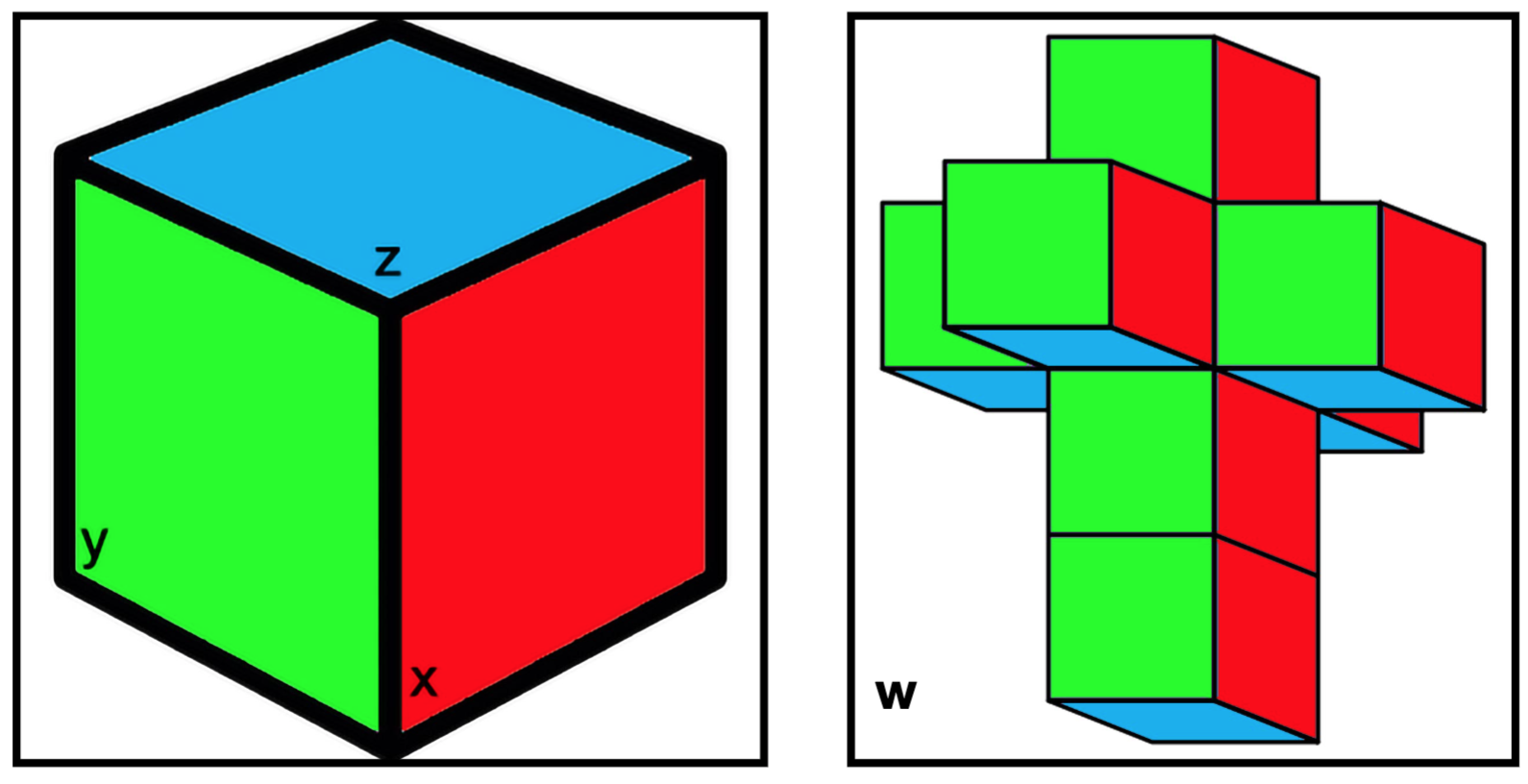
Fig 21: Left: The vertex-first projection of a ‘u’ quark in 3D. Right: The hypercube net of ‘u’ quarks.

If we look at the u quark in Fig. 21, we see that the parallel faces in-line with the x-axis are coloured red, those in-line with the y-axis are green and the z-axis is blue. These are the three colour charges of the quark and a rotation about any of these aforementioned axes — from the point of view of a preferred axis — will result in a colour change. However, every single one of the 8 cubes that go into making up the u quark hypercube looks the same and is orientated the same. This means that no matter which way it is turned about the w-axis, the quark (from our perspective) will always look the same. In this sense, we can think of the matrix that describes the rotation in the w-axis as its identity matrix.

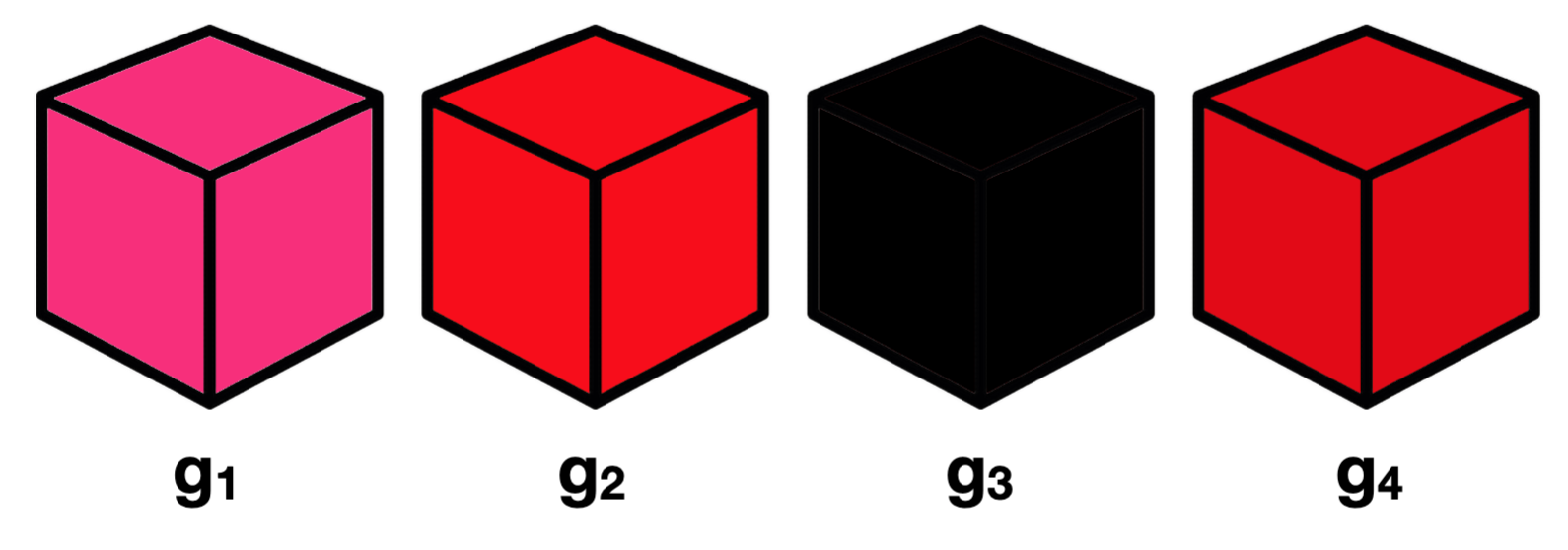
Fig 22.1: Gluons g₁ to g₄

On the other hand, if we were to rotate our RD gluonic structure in any combination of dimensions x, y or z, we won’t see any change in the colour of our gluonic cube. In a sense, these 3 dimensions collapse down to form our second identity matrix, this time for the RD gluons. While we can no longer see the fourth dimension, we are still imbued with the power to rotate our gluonic cube in that dimension. So, let’s do that with the help of our hypercube net (see Fig. 23).

Rotating our 4-D gluonic cube in any direction about the w-axis, will necessarily produce a colour change. Since it is the gluons that determine the colour change of the quarks in this model, the RD gluonic structure needs to rotate twice. Once in the w-axis and once in the plane of its ‘identity matrix’. Since its identity matrix is equivalent to the three rotational dimensions of the quark a rotation in these dimensions will necessarily result in a colour-change in the quark — just as a set of 4-dimensional cogs turning against one another produces a rotation one to the other.

Fig 23: Hypercube net of gluons with appropriate colour and anti-colour charges represented. g₁ is located at the centre of the cross, just below g₇

The reader may be surprised to learn that the colours of the gluons (in Fig. 22.1, 22.2, & 23) are not arbitrary. They are actually the linear addition, subtraction and multiplication of gluon colour charges;

g₁ = (red*yellow)+(blue*cyan) = RGB(253,32,121), CMYK(0,87,52,1)

This may be taking the colour analogy a bit too literally, but since we began in this mode, I thought we might as well continue with it.

To actually figure out how our model relates to say the colour charges of a neutron requires a lot of work. The basis states have to be known in advance and all of the subsequent rotations based on SU(3) have to be worked out separately before a consistent model can be constructed. And even then, all that work would amount to is a handful of dimensional gluon rotations in the w-axis. Perhaps something interesting might result from knowing these rotations, but this is highly unlikely and therefore it is an investigation best left for another time.

Thoughts & Connections

Instead, I’m just going to present some thoughts and connections between various mathematical values present both in the Gell-Mann matrices, the Rhombic-Dodecahedron and other various constants and values in Quantum Physics. In 8 (Fig 18) we see √3 preceding the matrix, while √2 is a persistent quantity used when deriving probabilities with SU(2) and SU(3) (Fig. 19). √3 has the value; 1.73205… which always reminds me of the mass of top and anti-top quarks: 173.1 GeV/c. This is obviously a red herring.

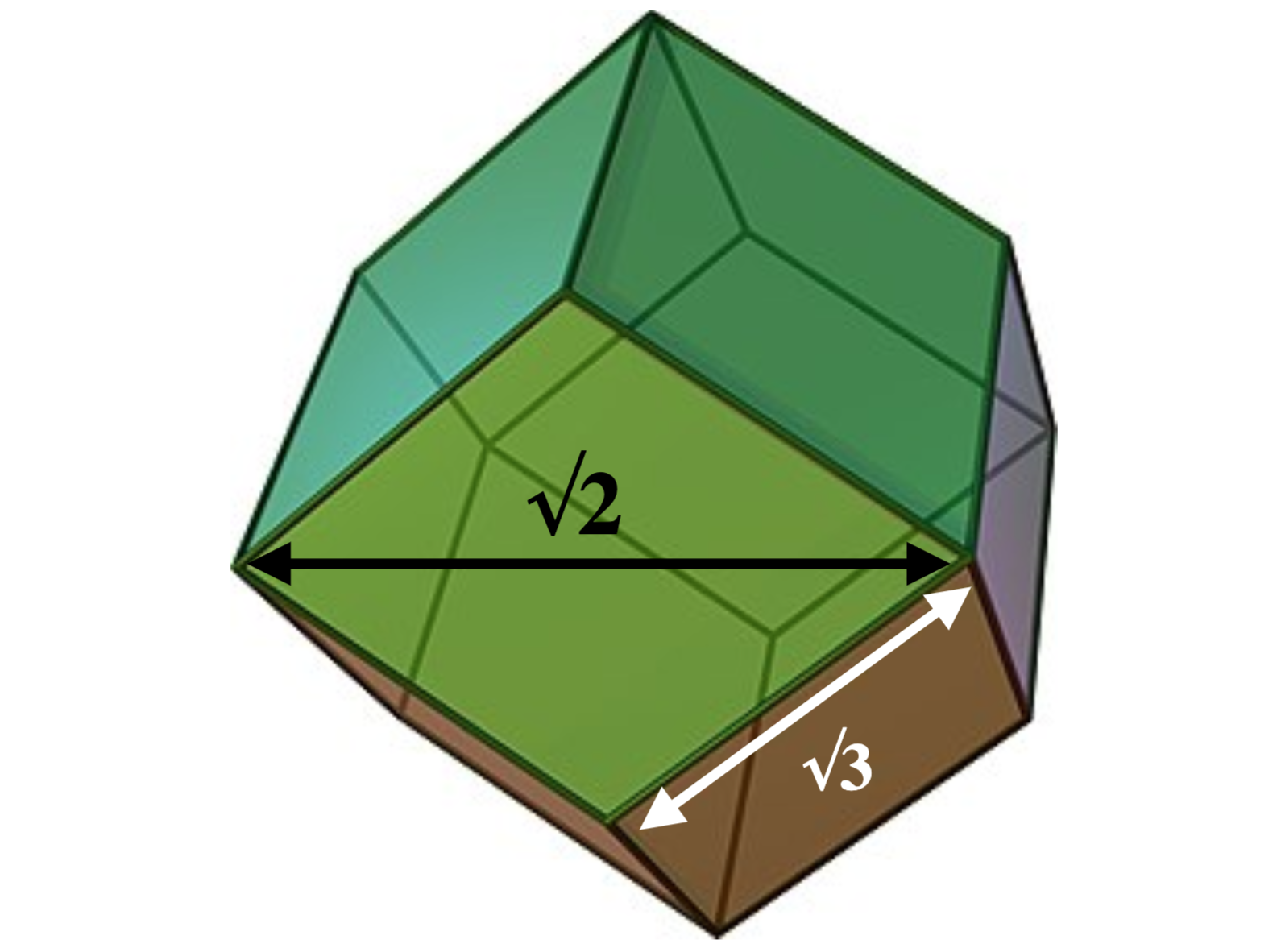
It is interesting to note, however, that √3 and √2 make an appearance in the structure of the Rhombi-dodecahedron (RD). The long diagonal of any one of the faces on the Rhombic-dodecahedron is √2 times that of the short diagonal. And the length of any of the edges is √3. (See Fig. 24) Such values are consistently seen in many regular polyhedrons, so it is not too surprising. However, it has been suggested elsewhere that the geometry of the rhombic-dodecahedron could find application in the error correcting codes of Quantum Computing.[7] Perhaps a similar kind of error correction maintains the colour charges and changes seen inside the nucleon. 

It may also be of further interest to note that the other angle present in the RD amounts to arctan(1/3). Arctan is consistently used to find the direction  (or angle) imposed on a charged object based on the vectors of other charged bodies, which—I suggest—is the reason it makes an appearance here. [8] If we add up the absolute value of all the charges of the particles in the Standard Model, we get 14, this is equal to the number of vertices in the rhombi dodecahedron.

arctan(1/3)

arctan(1/3)

The value ±1/3 directly relates to the charges of the d, s, b quarks and their anti-particle counterparts. With arctan, as we know, relating to the angle of attraction between these particles. There are four such arctan(±1/3) angles around a vertex, making ±4/3. The hypothetical X-boson particle has a theoretical charge of ±4/3.  With 6 such angles total in the RD, this makes for the possibility of particles up to ±24/3 charge, or charge ±8. This is not the charge of the gluons themselves (of which there are 8), as they have no charge, but rather it is the source of all charges and charge values (the 14 vertices). This should not be a surprise, since the constituent force of the gluons (the Strong Force) is the last force to be unified and so was the first force to distinguish itself — sometime between the creation of the Universe and 10^-53 seconds of inflation.

Fig 26: The Cheshire Cat by John Tenniel (1865)

Finally, while the Cheshire Cat makes no mention of a ‘vertex-first projection perspective of a hypercube’ that I can find at least, it is clear that Lewis Carroll (Charles Dodgson) makes many allusions to the bizarre and dizzying aspects of non-Euclidean geometries, where size and proportions can change rapidly. Dodgson’s ‘Alice in Wonderland’ was intended to be a scathing and humorous criticism of this new way of thinking. [9] Maybe this is what the Cheshire Cat was referring to when he says to Alice; “… we’re all mad here. I'm mad. You're mad.” When Alice asks how the cat knows, she’s mad, which is ironic in itself, he says: “You must be… or you wouldn't have come here.” [10]

Obviously, I couldn’t disagree more. There are few pursuits more sane and sane-making, in my opinion, than attempting to work out the geometric rotations of objects in higher dimensional spaces. If I had to look for an analogy, I would liken it to the practice of devout meditation. And what could be more sane or sane-making than that?

Conclusion

We have been able to relate the 8 gluons of SU(3) to the eight cubes of the tesseract, which is itself always been our model for the gluons, in the form of a 4-dimensional quaternionic rhombic-dodecahedron. In doing so, we have discovered that each gluon field looks like some kind of hexahedron or rhombohedron, depending on the angle of view. Using the gluonic-quaternions, we were easily able to model the flux tube, which mediates quark confinement. It was inconclusive, as to whether or not the gluon undergoes rotation ,when stretched and therefore whether it is the ‘jiggling’ of the quarks inside of the Strong Force that creates the quark and gluon colour charges. Further research will shed light on this.

Citations

[1] ‘DGO Quaternion Multiplication, Quarks and Polyhedra’, Christopher C. O’Neill: https://www.researchgate.net/publication/347495967_DGO_Quaternion_Multiplication_Quarks_Polyhedra

[2] ‘Logic Gate Arithmetic and Quaternions’, Christopher C. O’Neill:

https://www.researchgate.net/publication/347435053_Logic_Gate_Arithmetic_and_Quaternions

[3] https://en.wikipedia.org/wiki/Rhombic_dodecahedron#/media/File:Hypercubeorder.svg

[4] https://commons.wikimedia.org/wiki/File:Hypercubeorder_binary.svg

[5]http://www.physics.adelaide.edu.au/theory/staff/leinweber/VisualQCD/Nobel/

[6] https://math.ucr.edu/home/baez/physics/ParticleAndNuclear/gluons.html

[7] ‘The surface code on the rhombic dodecahedron’, Andrew J. Landahl: https://arxiv.org/pdf/2010.06628.pdf

[8] https://www.kpu.ca/sites/default/files/Faculty%20of%20Science%20&%20Horticulture/Physics/PHYS%201100%20Electric%20Fields%20Solutions.pdf

[9] ‘The Hidden Math Behind Alice in Wonderland’, Keith Devlin; https://www.maa.org/external_archive/devlin/devlin_03_10.html

[10] https://www.cs.cmu.edu/~rgs/alice-VI.html