Entanglement

The fundamental principles of entanglement are re-examined from the perspective of Dimensional Gate Operators. This brings to light the possibility that entanglement is itself a type of emergent property and provides an avenue where hidden variables may play a role after all. Testable predictions are discussed, which might lead to a new understanding of the underlying processes of space-time and reality.

Entanglement

Our understanding of quantum entanglement has greatly improved over the last number of decades, especially in regard to the number of particles that are entangled or separable in an ensemble of particles. This application is especially useful in quantum computing. But our understanding of the mechanism that produces the entanglement is less advanced. The reason for this lack of advancement is possibly two-fold. In the first instance, it would appear that the impetus for its discovery simply isn’t there, as no new forms of products or technology could come from such an explanation, so why bother funding it? Secondly, and possibly more likely, is the difficultly of the problem itself.

To address the first issue first, I would say that it is in our interest to investigate such phenomena, since that is the role and the domain of researchers and scientists. The pursuit of knowledge is worthwhile in itself and will lead to its own rewards. As to the second issue, I hope to dispel some of the confusion surrounding the subject of entanglement via the application of Dimensional Gate Operators (DGO), which appear to have proven their ability to address other intractable problems in Quantum Physics and mathematics in the past and in past papers.

Currently, our best explanation states that when two particles become entangled, they share the same wave function and therefore, a change in the state of one particle immediately produces a change in the other, no matter the distance between them. I don’t dispute this as a possibility, but so far I am unaware of the precise mechanism, which provides for this one wave function to generate such opposite effects in its partner particle. DGO, on the other hand, easily decides this and without the need for any extra assumptions outside of DGO itself, which is a very promising aspect of the hypothesis, in general. Quantum Entanglement occurs in different forms under numerous different situations. But, the one we will focus on is the one that is most commonly referred to i.e. electron pair creation. When particles are generated they are always generated in entangled matter and anti-matter pairs. Measurement of the spin of a particle on one axis immediately determines the spin of the other, so long as the two particles remain entangled. This form of non-locality should be impossible under Special Relativity. But there is an obvious resolution to the problem, which comes from the momentum and position of each particle.

The momentum p of a particle is defined by:

p = mv

where m is the mass of the particle and v is it’s velocity. The position of a particle is contained within it’s velocity, so we can see that these are interdependent and related properties i.e. a change in one can result in a change in the other:

p = m(d(x)/dt)

Suppose we have two entangled particles A and B. The position variable of each particle is x1, and x2, where x1 = 1 and x2 = -1. The momentum of each particle is by extension p1, and p2.

p1 = m(d(x1)/dt)

p2 = m(d(x2)/dt)

If the mass of our electron is 3, for simplicities sake, then the momentum for each particle, after one second of travel, can be determined both in the XNOR(!∆) and XOR(∆) dimension gates, as follows:

p1 = ∆(3(d(1)/d(1)) = 3

p2 = !∆(3(d(-1)/d(1)) = -3

As we can see p2 has a negative momentum, which is an expected result since both particles are moving away from each other from a fixed point. If we arrange the properties of our two particles in a grid form, we can examine the state of our particles before entanglement (if that is the case), during the process and the after the entanglement has occurred:

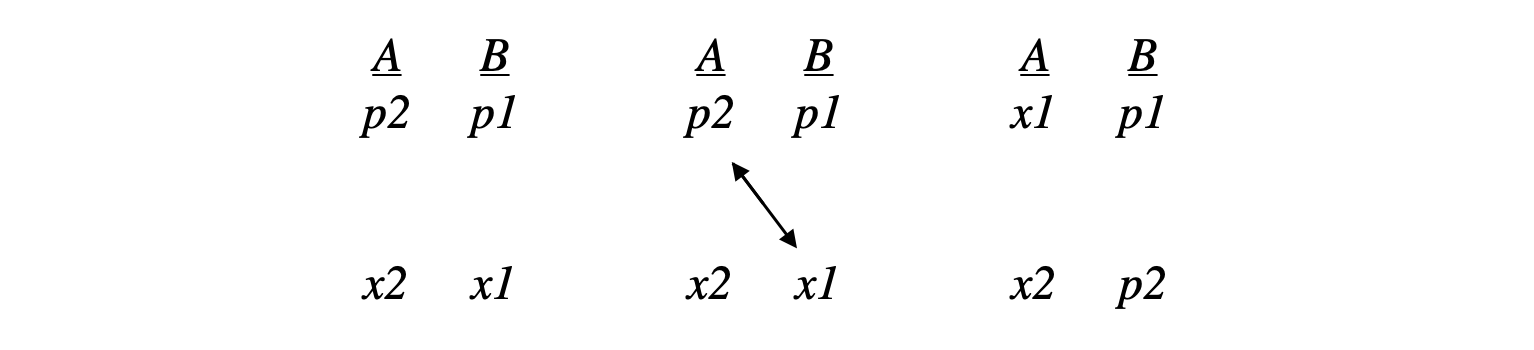
On the left, we see our two electrons A and B and their respective properties arranged in a column beneath them. This is the state they are in before entanglement. During the process of entanglement, when both particles are in contact with one another, particle A transfers its momentum information to particle B and displaces its position information in the process. Finally, on the right, we have our two newly entangled particles that share the position information for each particle A and B.

This explains why the two particles are in constant communication with each other, as they literally have the position information of the other hard-coded into their respective XNOR and XOR registers, thus they have continuous and updated information on where the other particle is at all times. If you think this smacks too much of the EPR Hidden Variable hypothesis, hold on, I’ll get to that in the next section.

As we know, or as we have seen in previous editions of DGO, the particle information is determined by XNOR and the position by XOR. It doesn’t have to be this way, but it is good to keep things consistent. Our x1 information is increase by +=1 every second. But once it switches to XNOR, this becomes -=1. Similarly, the momentum state is set to decrease, as per equation !∆(3(d(-1)/d(1)), but once it goes to the XOR space, this naturally begins to increase.

∆!(x1)/∆(x2)

∆!(p1)/∆(p2)

After t=5, we see that x1 = -5, x2 = -5, p1 = 5 and p2 = 5. The important thing to note here is that both x1 and x2 are negative and p1 and p2 are positive.

At t=6, the spin of particle A is measured along the y-axis and determined to be in the spin state +1. This value is the result of dividing the two different states of the same particles, which are always exactly equivalent, in their respective XNOR or XOR spaces, like so;

A: ∆((x1)/(x2)) = 1

B: !∆((p1)/(p2)) = -1

Immediately, there is a decoherence and the other particle is seen to be spin-1. What determines the spins of the two particles? Is it the measurement device, which is obviously in XOR?

That’s a reasonable assumption, but there is something else to consider here. Recall that p1 and p2 are correlated with XNOR, while x1 and x2 correlate with XOR. The imbalance of the momentum-states and position-states being in either all one particle or the other determines the outcome. And as we have seen, which of the two particles gets all of the position-state information, or all of the momentum-state information is determined at the beginning, when the two particles A and B come into contact with each other. This process is entirely random, as you would expect and so there is no way to know which particle will be the spin up and which the spin down, before they are measured.

Once, they are measured however, the x1 information ceases to be calculated in XNOR and moves from -=1 to +=1 and when this happens it gets snapped out of the XNOR register and deposited back into the XOR register, from where it originally came. A similar process occurs in the opposite direction for the p2 information. This separation occurs, because of the impossibility of particle A being in momentum-state XNOR with the vector information of the position-state XOR.

This means that they become two separate, discontinuous equations, which cannot be differentiated as lim goes to 0:

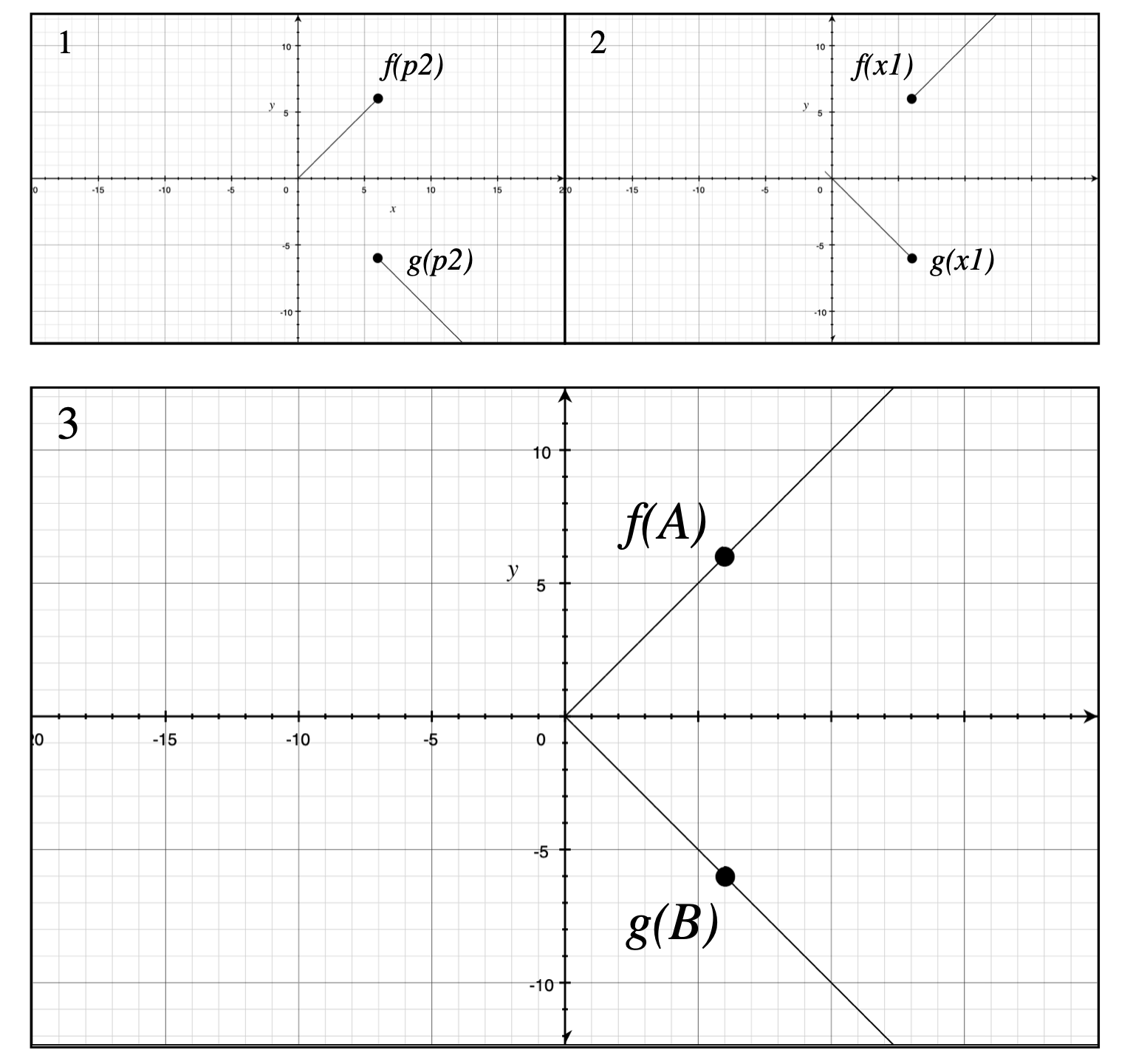
Figure 1: The discontinuous functions f and g for p2, before and after decoherence, represented by the black dot. Figure 2: The discontinuous functions f and g for x2, before and after decoherence.Figure 3: The superposition of p2 and x2, which represents the totality of the trajectories of the entangled particles A and B.

The discontinuous functions f(p2) and g(p2) in Fig 1 cannot be differentiated beyond the point of disentanglement, represented by the black dot. This is also true of the functions in Fig 2. The inability of the equation being differentiated beyond this point is representative, or indicative, of the separation of the entanglement from the XNOR to the XOR space and vice versa.

Differentiating these simple functions prior to and after their respective limits produces the following series of equations:

This is all fairly straight forward. But it leads to a new perspective on quantum entanglement, which is that the wave functions prior to and after measurement are emergent properties. What kind of emergence? Strong or weak? No, these terms are not directly applicable to Quantum Mechanics under the DGO model. Instead we use the term High-Emergence, because while we do not have access to the underlying mechanism, we can still infer its constituent elements via our own mathematical axioms. By contrast, Low-Emergence would be a physical system whose effects we can observe, but whose properties we cannot derive from our axioms. I cannot think of an example of this — unless you want to consider sum total of physical and metaphysical properties that, as yet, we have no account for e.g. consciousness.

For completeness sake, I will give the reverse of our previous example:

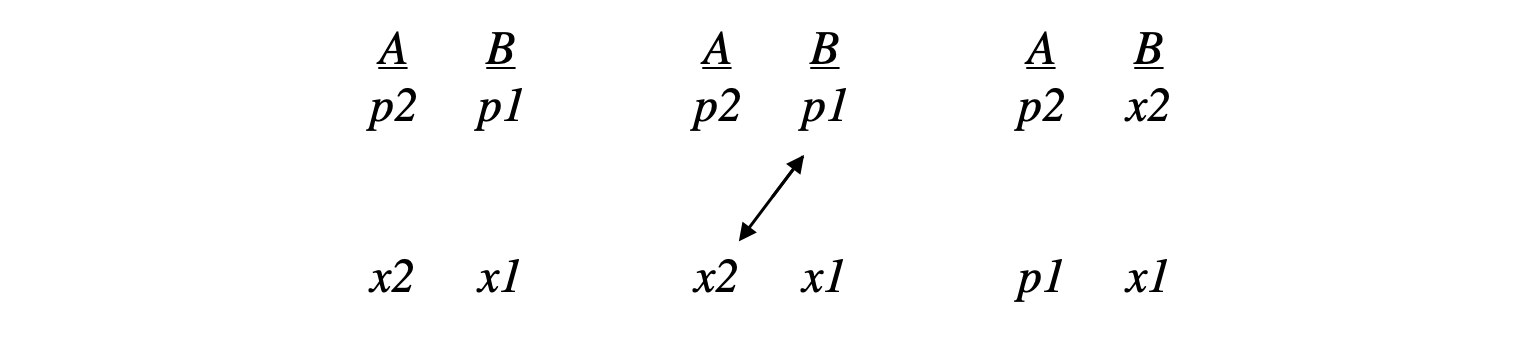
, which leads to:

∆!(p2)/∆(p1)

∆!(x2)/∆(x1)

Here, x1 and x2 are now both positive and p2 is p1 are both negative. After decoherence, we have our spin ups and spin downs reversed, compared to how they were in equations (9) and (10):

A: !∆((p2)/(p1)) = -1

B: ∆((x2)/(x1)) = 1

As we have seen and as we know, the spins are randomly predetermined ahead of time. So does this mean that hidden variables are in some sense true? And if so, where does that leave non-locality and Bell’s Inequality theorem?

Hidden Variables

Quantum Entanglement posed a major concern to physicists in the early-20th Century, as it appeared to violate the precepts of Special Relativity. The EPR Paradox was intended to do away with the apparent non-locality of the system in favour of ‘hidden variables’. Hidden variables — it was believed — would account for how a particle was to behave under certain circumstances. These variables were thought to be preset or ’hardcoded’ into the fabric of the particle itself.

In 1964, an Irish physicists named John Bell suggested a means to test the validity of the hidden variables postulate. This became known as Bell’s Inequality Theorem. These experiments are mostly concerned with entangled photons passing through polarised filters set at different angles. After repeated experimentation, hidden variables have been almost entirely ruled out and the principle of non-locality has emerged victorious.

I believe that the DGO model of entanglement confirms the non-local model, in fact, it seems to go further suggesting that, on the level of the entangled particle, information about its position is being shared and teleported across space and time at all instances prior to and up to the moment of decoherence. This appears to contravene Special Relativity, which precludes information travelling faster than the speed of light. However given that this information is Highly-Emergent and therefore not in any useable form it does not effect the observer in any real, or detrimental way i.e. no time paradoxes.

Furthermore, DGO lends some credence to the idea of Hidden Variables, although not in the way that EPR would probably have hoped for. The variables of the entanglement are preset at the moment of entanglement, but there is no way to know what they are until they are measured. Furthermore, it offers no further insight or resolution to the problem of which entangled photon passes through which polarised filter or not.

Why would it?

After all, these kinds of experiments are incapable of testing any observable aspect of non-locality and are primarily concerned with probabilities. The solution to these polarised light experiments is most likely to be found in sweet-spots, or notches, of dimensionality around 3 and 4 or some other characteristic of polarised wave functions, all of which are outside the scope of this paper.

Testable Predictions?

As for what kind of testable predictions this could lead to, this is far from clear and the fact that the system is Highly-Emergent means that tests of this kind may be an inherent impossibility.

My feeling is that a physical system that switches from one Dimension Gate state to another instantly upon measurement must undergo extreme forces, not unlike a wheel that is spinning in one direction only to be stopped and spun in the other. These forces may simply manifest as the various opposite spin-states of the separated particles themselves, in which case, we are back to square one. But they may also produce a violent collision point and subsequent opposite reaction, as per Newtonian Physics. Then again, perhaps this way of thinking is simply too ‘classical’.

Alternatively, it could be that there are no forces acting on the particle and that it simply zips through one boundary of the Dimensional Gate Operators and into the other smoothly, without any perturbation. If this is the case, then it means that the position and momentum of a particle is directly linked to the coordinate geometry of space and is in some sense non-material, as much as it is non-local. In other words, the whole process acts like some kind of carefully crafted illusion or ‘Magician’s Trick’. To understand exactly what I mean by this, look again and Figures 1 and 2, which — from the point of view of a quantum particle — looks very much akin to a Magician pulling a rabbit out of a hat.

Conclusion

In conclusion, DGO offers a self-contained and lucid explanation of the mechanics behind entanglement. The hypothesis is in line with Bell’s Inequality and even resurrects Hidden Variables, to some extent. These hidden variables suggests that quantum entanglement has High-Emergent characteristics. However, these same emergent characteristics appear to preclude any and all testing of the hypothesis, as we cannot peer into the inner-workings of the entanglement without changing the result itself. However, if we were to grant the DGO Entanglement hypothesis, then close observation of the particle at the moment at which decoherence occurs might tell us something about the structure of the Universe and the fabric of space and time itself. If the transition is smooth and not at all jagged then it could suggest that there is an underlying spatial coordinate system and that material reality is akin to some computational illusion. While these ideas might not sit well with reductionists and physicalists, but there is no doubt that they could offer a tantalising perspective on the universe, if proven true.